Решение: Обозначим объём вспашки всего поля за 1(единицу), а время вспашки всего поля Иваном за (х) часов, тогда время вспашки поля Григорием, согласно условия задачи, равно: (х+6) час Производительность работы Ивана в 1 час 1/х; Производительность работы Григория в 1 час 1/(х+6) А так как работая вместе они вспашут поле за 4 часа, то: 1 : [1/х/(х+6)]=4 1: [(х+6+х)/(х²+6х)]=4 1 : [(2х+6)/(х²+6х)]=4 х²+6х=(2х+6)*4 х²+6х=8х+24 х²+6х-8х-24=0 х²-2х-24=0 х1,2=(2+-D)/2*1 D=√(4-4*1*-24)=√(4+96)=√100=10 х1,2=(2+-10)/2 х1=(2+10)/2 х1=6 х2=(2-10)/2 х2=-4 - не соответствует условию задачи Время вспашки поля Иваном составляет 6 часов
Тут нужно решать интервальным методом, показать здесь я это не могу. Но для начала нужно найти нули функции(значения х, при котором функция была бы равна нулю). Здесь нули ф.: 4;-3,5. Затем чертим ось ох, обозначаем эти точки и участки, где функция положительна или отрицательна. В итоге получаем, что функция <0 при х принадлежащем отрезку (-3,5;4) 2 решается точно так же, но тут для удобства нужно в 1 скобуе поменять местами числа, затем вынести за скобки -1 и умножить обе части неравенства на -1(при этом знак> меняется на знак <). Вот что получается (х-2)(х+1)<0. Нули функции: 2;-1. Дальше как я уже объяснял выше. ответ: при х принадлежащем отрезку (-1;2)
(см. объяснение)
Объяснение:
Понятно, что D(y)=x≥-2. Тогда E(y)=[2; +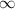 ).
).
Задание выполнено!