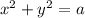
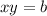
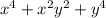
Пусть взяли х л 30%-го раствора соли. Тогда (3-х) л взяли 23%-го раствора соли. Чистой соли в первом растворе 0,3х л, а во втором 0,23(3-х). По условию известно, что концентрация соли в новом растворе равна 27%, т.е. соли в нем 0,27·3 = 0,81 л.
При смешивании двух растворов соли объем чистой соли в новом растворе можно получить сложением объемов соли в первоначальных двух растворах.
0,3х + 0,23(3-х) = 0,81
30х + 23(3-х) = 81
30х +69 - 23х = 81
7х = 12
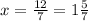
Значит, взято было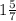 
литров 30%-го раствора соли.
ответ: 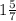л.
43 (л) жидкости в первой ёмкости.
41 (л) жидкости во 2 ёмкости.
Объяснение:
В первой ёмкости на 2 л жидкости больше, чем во второй.
Если из первой ёмкости перелить во вторую 15 л жидкости, то во второй ёмкости станет в 2 раза больше, чем останется в первой.
Сколько литров жидкости в каждой ёмкости?
х - литров жидкости во 2 ёмкости.
х+2 - литров жидкости в первой ёмкости.
х+15 - литров жидкости стало бы после переливания во 2 ёмкости.
(х+2)-15 - литров жидкости стало бы после переливания в 1 ёмкости.
Согласно условию задачи, во второй ёмкости после переливания станет жидкости в 2 раза больше, уравнение:
2*[x+2)-15]=х+15
2(х-13)=х+15
2х-26=х+15
2х-х=15+26
х=41 (л) жидкости во 2 ёмкости.
41+2=43 (л) жидкости в первой ёмкости.
Проверка:
43-15=28 (л) стало бы жидкости в первой ёмкости после переливания.
41+15=56 (л) стало бы жидкости во второй ёмкости после переливания.
56 : 28 = 2 (раза), верно.