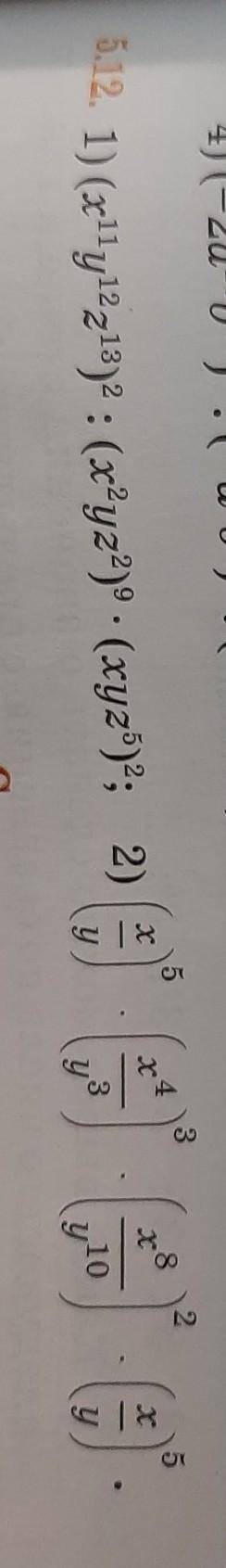
Решение системы уравнений х₁=1 х₂= -3
у₁= -3 у₂=1
Объяснение:
х+у= -2
х²-2ху+у²=16 в левой части развёрнут квадрат разности, свернуть:
х+у= -2
(х-у)²=16
Выразим х через у в первом уравнении, подставим выражение во второе уравнение и вычислим у:
х= -2-у
( -2-у-у)²=16
( -2-2у)²=16 разворачиваем квадрат разности:
(-2)²-2(-2*2у)+(2у)²=16
4+8у+4у²-16=0
4у²+8х-12=0/4
у²+2х-3=0, квадратное уравнение, ищем корни:
у₁,₂=(-2±√4+12)/2
у₁,₂=(-2±√16)/2
у₁,₂=(-2±4)/2
у₁= -6/2
у₁= -3
у₂=2/2
у₂=1
х= -2-у
х₁= -2-у₁
х₁= -2-(-3)
х₁= -2+3
х₁=1
х₂= -2-у₂
х₂= -2-1
х₂= -3
Решение системы уравнений х₁=1 х₂= -3
у₁= -3 у₂=1
1) -3х+6у-12х-9у= -15x-3y
2) 6mn-2m-11mn-3n-5m=-5mn-7m-3n
1) (3a-7b)-(4a+8b)= 3a-7b-4a-8b=-a-15b
2)-(5m-7n)+(2n+12m)=-5m+7n+2n+12m=7m+9n
3) 3x(1-4x)-5x(6x+7) =3x-12x-30x-35x=-74x
4) 5c(2c+a)+(3c-2a)(5a-2c)=10c^2+5ca+15ca+6c^2-10a^2+4ca=16c^2+24ca-10a^2
5) (5y-3) куб. -(2-5y)куб=125y^3-225y^2+45y-27-8+150y - 60y^2+125y^3 =250y^3-285y^2+195y-32
1) 13(а-2)+10(4-а)=23
13a-26+40-10a=23
3a=9
a=3
2) (2х-1)(х+1)-х куб.=(х-3)куб -10
2x^2+2x-x-1-x^3=x^3-6x^2+27x-10
8x^2-28x-2x^3=-9
x(8x-28-2x^2)=-9
x1=0 (8x-28-2x^2)=-9
-2x^2+8x-19=0
D=8^2-4*(-2)-(-19)=-88(нет корней)
ответ:0
3) x/4 + x/8 =3/2
3x/8=3/2
3x=8*3/2
3x=12
x=4
В решении.
Объяснение:
1) (х¹¹у¹²z¹³)² : (х²уz²)⁹ * (хуz⁵)²=х⁶у¹⁷z¹⁸.
1)Возвести в степень (показатели степеней перемножаются):
(х¹¹у¹²z¹³)² : (х²уz²)⁹ * (хуz⁵)²=
=(х²²у²⁴z²⁶) : (х¹⁸у⁹z¹⁸) * (х²у²z¹⁰);
2)Деление:
(х²²у²⁴z²⁶) : (х¹⁸у⁹z¹⁸)=
при делении показатели степеней вычитаются (при одинаковых основаниях):
=х²²⁻¹⁸у²⁴⁻⁹z²⁶⁻¹⁸=
=х⁴у¹⁵z⁸;
3)Умножение:
(х⁴у¹⁵z⁸) * (х²у²z¹⁰)=
при умножении показатели степеней складываются (при одинаковых основаниях):
=х⁴⁺²у¹⁵⁺²z⁸⁺¹⁰=
=х⁶у¹⁷z¹⁸.
2) (х/у)⁵ * (х⁴/у³)³ * (х⁸/у¹⁰)² * (х/у)⁵=
1)Возвести в степень (правило то же, что и в первом примере). При возведении дроби в степень возводить в степень и числитель и знаменатель.
(х⁵/у⁵) * (х¹²/у⁹) * (х¹⁶/у²⁰) * (х⁵/у⁵)=
=(х⁵*х¹²*х¹⁶*х⁵) / (у⁵*у⁹*у²⁰*у⁵)=
=х⁵⁺¹²⁺¹⁶⁺⁵/у⁵⁺⁹⁺²⁰⁺⁵=
=х³⁸/у³⁹.
(х в 38 степени, у в 39 степени, если нечётко видно).