№1
хₙ=(3/(-1))ⁿ=(-3)ⁿ
х₁=(-3)¹=-3
х₂=(-3)²=9
х₃=(-3)³=-27
х₄=(-3)⁴=81
х₅=(-3)⁵=-243
Чтобы получить следующий член, предыдущий умножаем на (-3).
№2
хₙ=(1/2)ⁿ + 2ⁿ=2ⁿ + (1/2)ⁿ
х₁=2¹ + (1/2)¹=2 1/2
х₂=2² + (1/2)²=4 + 1/4=4 1/4
х₃=8 1/8; х₄=16 1/16; х₅=32 1/32.
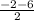 = -4
= -4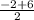 =
= 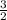 = 1,5
= 1,5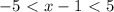
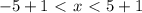
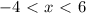
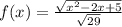 :
: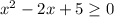
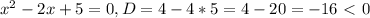
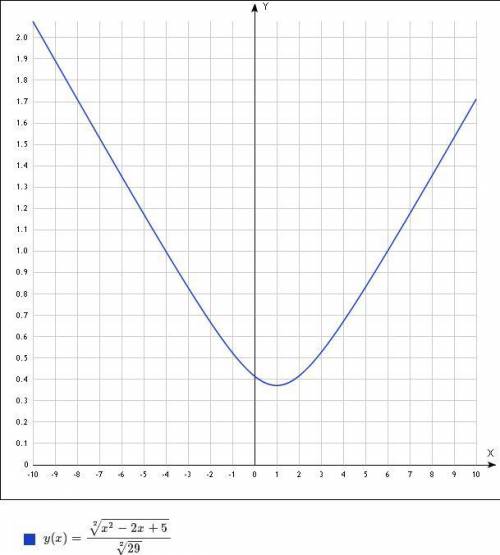
 - парабола ветвями вверх, то неравенство выполняется для любых х.
- парабола ветвями вверх, то неравенство выполняется для любых х.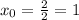
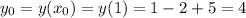
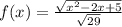 принимает в вершине параболы х=1:
принимает в вершине параболы х=1: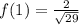
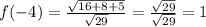
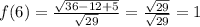
хₙ=(-3)ⁿ
х₁=-3; х₂=9; х₃=-37; х₄=81;х₅=-243
хₙ=(1/2)ⁿ+2ⁿ
х₁=2 1/2
х₂=4 1/4
х₃= 8 1/8
х₄= 16 1/16
х₅=32 1/32