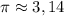{-25y+x=-12,8 {x=1,2-y можно решение( - id1385027220220306 от Lol11111111000 06.03.2022 19:51

Question

Алгебра: {-25y+x=-12,8 {x=1,2-y можно решение(​

Lol11111111000 · Accepted Answer

Тут можно разными Есть как минимум
1) зная, что $\pi\approx 3,14$ прикинуть, чему равно 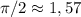$\pi/2\approx1,57$ . Ну, и исходя из этого, сразу видно, какое должно быть k, В этом примере как раз 1,57+3,14=4,71. Т.е. при k=1 попадает в интервал. Следующий корень уже будет 4,71+3,14=7,85, т.е. уже точно выходит за интервал. Поэтому при k=2 в интервал не попадает. Но все это годится в примерах, когда числа небольшие, и все очевидно на глаз.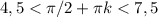
2) Самый точный составить неравенство, задающие условие на k, а именно, по условию должно быть
4,5

Решаем его:
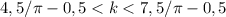
$4,5/\pi-0,5$
с округлением, скажем, до 2-х знаков:
0,93

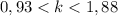. Т.е. видно, что возможно только одно целое k=1.

{-25y+x=-12,8{x=1,2-yможно решение(​

MOGZ ответил

{-25y+x=-12,8
{x=1,2-y
можно решение(