опишу в общем виде: составляешь таблицу со строками «туда» и «обратно». Там расстояние (S) будет одинаковое, скорость (v) «туда» обозначим за х, а скорость «обратно» за х+2. Время «t» выражаем через формулы скорости v=S/t, НО! Во времени «обратно» ещё добавляем два отдельно от дроби. Дальше составляем уравнение и домножаем каждую дробь и двойку на х(х+2), то есть приводим к общему знаменателю-единице. Раскрываем скобки, сокращаем, получившее квадратное уравнение -2х^2-4х+448=0 делим на -2 и получаем х^2+2х-224=0. Через дискриминант (равный 900) решаем уравнение, получаем корни 14 и -16. -16 не подходит, потому что скорость не может быть отрицательной. Прибавляем к 14 два (по условию) и получаем 16. Вторую хз как решать

1. а) 6а2(а-2б+3)
б) (х-3)(х-2) так по-моему
2. а) у(х+3)+z(х+3) = (у+z)(х+3)
б) (5а-с)(5а+3)
в) с(б2+2бс+с2) = с(б+с)2
3. х/у (сокращаешь у2, остается ху/у2, сокращаешь у и у2)
4. а2-2а-(а2-1) = а2-а2-а2+1
5. Два множителя, два уравнения:
х-5 = 0 или 2х+8 = 0
х = 5 х = -4
ответ: 5; -4
6. с(с2-4)-с3-1 = с3-4с-с3-1 = -4с-1
7. 3х(х2-9) = 0
3х(х-3)(х+3)
3х = 0 или х-3 = 0 или х+3 = 0
х = 0 или х = 3 или х = -3
ответ: 0; 3; -3
8. 2(х+у)-(х-2ху-у2) = 2(х+у)-х+2ху+у2 = 2(х+у)-(х+у)2 = 2(х+у)(х+у+1)
а 9 со звездочкой :(
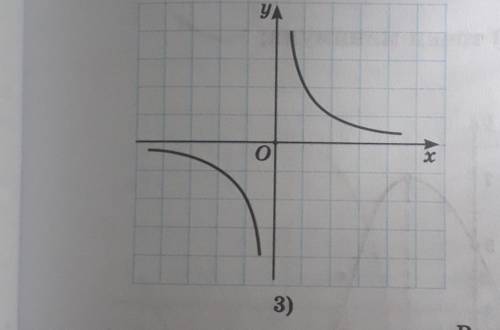
Объяснение:
обл. определения D(f)=(-∞;0)∪(0;+∞)
обл. значения E(f)=(-∞;0)∪(0;+∞)
т.к. график не пнресекает ось х, то функция нулей не имеет
при х∈(-∞;0) функция убывает от 0 до -∞; при х∈(0;+∞) функция убывает от +∞ до 0