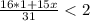
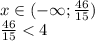УМОЛЯЮ ОЧЕНЬ НАДО!! Докажите формулу (ab):c=a*(b:c) Используйте геометрическое обоснование и рисунок - id1387431420210622 от killfa 22.06.2021 22:56

Question

Алгебра: УМОЛЯЮ ОЧЕНЬ НАДО!! Докажите формулу (ab):c=a*(b:c) Используйте геометрическое обоснование и рисунок 3.

killfa · Accepted Answer

1) Оценим сумму , для этого примем что есть равные числа. Так как есть место для чисел 3 4 и 6 это 3 числа.
$\frac{16*1+15x}{31}$
$x \in (-\infty;\frac{46}{15})\\ \frac{46}{15}$ то есть да может , так как 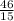$\frac{46}{15}$ ее целая часть равна 3 , а она натуральное число , и найдется набор таких чисел что среднее арифметическое будет меньше 2 , так как в условий не сказано что , сам набор может состоят так только из разных натуральных чисел.
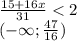2) $\frac{15+16x}{31}$ , целая часть этого числа равна

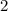, то есть не может , так как в сумме 2=1+1

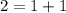, и по количеству в этом наборе минимальное есть 16 единиц .
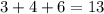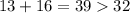3) $3+4+6=13\\$ так как мы ранее доказали что , есть не менее 16 единиц , и того 13+16=3932

что удовлетворяет условию .

УМОЛЯЮ ОЧЕНЬ НАДО!! Докажите формулу (ab):c=a*(b:c) Используйте геометрическое обоснование и рисунок 3.

MOGZ ответил