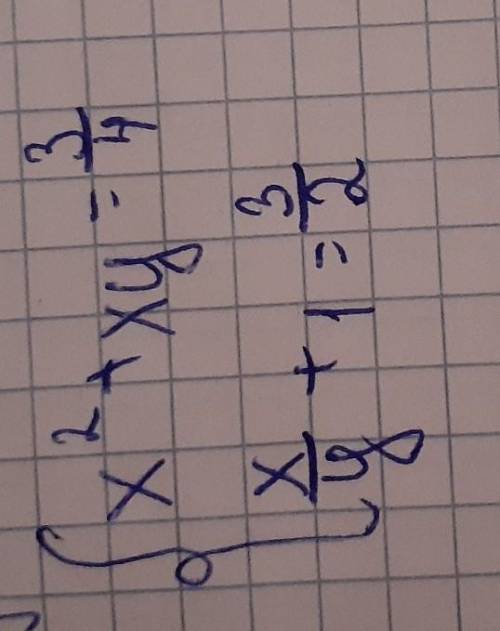
В решении.
Объяснение:
Задайте формулой функцию график которой проходит через точку
(0; 5) и параллелен графику функции у= -4х.
Дана функция: у = -4х;
Точка (0; 5);
Написать формулу функции, параллельной данной.
Графики линейных функций параллельны, если: k₁ = k₂, а b₁ ≠ b₂.
Значит, k₂ = -4;
Найти b₂ ( b₁ = 0):
Подставить в уравнение линейной функции у = kx + b известные значения х и у (координаты точки ) и вычислить значение b₂:
5 = -4 * 0 + b
5 = 0 + b
b₂ = 5;
Формула функции, параллельной данной: у = -4х + 5.
x = 1; y = 0
Объяснение:
к сожалению, у меня нет тетради под рукой, поэтому нашёл пересечение через symbolab, но я могу объяснить как сделать тоже самое, только на бумаге.
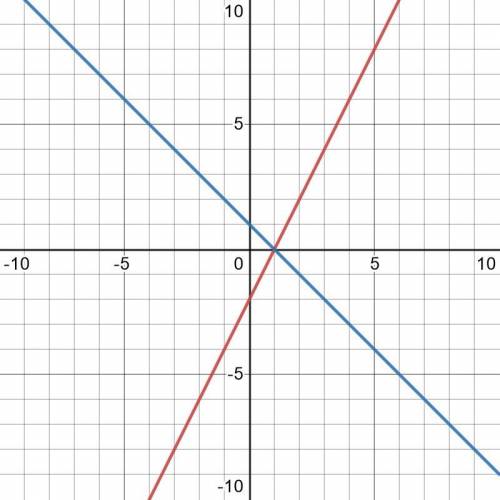
у нас две функции, у которых нужно найти точку пересечения.
обе функции вида 
, значит у них только одна точка пересечения, так как графики этих функций – бесконечные прямые.
Нужно найти лишь две точки, чтобы построить график линейной функции.
То есть придумываем любое удобное число и подставляеете в функцию вместо x, затем считаем и получаем значение y.
Например, 
вместо x подставляем любое число, я возьму 2
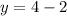
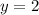
Мы получили, что 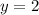, при 
Теперь находим такую точку, что , а на координатной плоскости.
Надеюсь, алгоритм построения графика линейной функции понятен
Объяснение:
........................................................................