x1=3
x2=1
Объяснение:
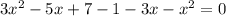
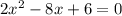
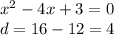
x=(4±2)/2
x1=3
x2=1
Решите уравнение
(X+1)^2/3-(X-1)/2=(8X-1)/6
(X+1)^2/3-(X-1)/2=(8X-1)/6 |*6
2(X+1)^2-3(X-1)=8X-1
2x^2+4x+2-3x+3-8x+1=0
2x^2-7x+6=0
D=49-4*2*6=1
x=1,5
x=2
Решите уравнение
(2X-3)^2-2(5X-4)(X+1)=-9-13X
(2X-3)^2-2(5X-4)(X+1)=-9-13X
4x^2-12x+9-2(5x^2+5x-4x-4)+9+13x=0
4x^2-12x+9-10x^2-10x+8x+8+9+13x=0
6x^2+x-26=0
D=1-4*6*(-26)=625
x=-13/6
x=2
Не вычисляя корней квадратного уравнения, решите уравнение
1) 3X^2-2X-6=0
y(первое)=3X^2-2X-6
y(второе)=0
найдем координаты вершины параболы:
x(в)=-b/2a=2/6=1/3
y(в)=3(1/3)^2-2(1/3)-6=-19/3
координаты:(-19/3)
x = 2; 3.
Объяснение:
3х^2 - 5х + 7 = 1 + 3х + х^2
Перенесем все в одну часть, меняя знаки при переносе.
3х^2 - x^2 - 5x - 3x + 7 - 1 = 0
2x^2 - 8x + 6 = 0
Решим через дискриминант.
D = b^2 - 4ac = 64 - 48 = 16.
x1 = (-b + sqrt(D)) / 2a = 8 + 4 / 4 = 3
x2 = (-b - sqrt(D)) / 2a = 8 - 4 / 4 = 2