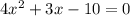, если их несколько, то указать сумму. 
): 
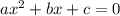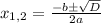, дискриминант же расписывается по-своему: 
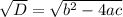. Дискриминант как бы заслужил своё отдельное внимание, ведь именно при его вычислении люди нередко допускают ошибки. Теперь – решаем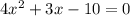, отсюда: 
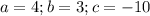, значит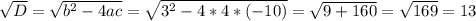
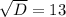; это как в алгебраических выражений седьмого класса – ты складываешь буквы, подставляешь вместо них какие-то числа и считываешь ответ, так вот здесь тоже самое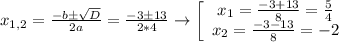
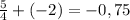
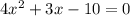равна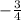 
1. записываем пример.
2. раскрываем формулу разности квадратов (x^2-y^2) и закрываем формулу квадрата разности (x^2-2xy+y^2) и одновременно с этим проводим другие действия. при раскрытии формулы разности квадратов получается (x-y)(x+y). при закрытии формулы квадрата разности получается (x-y)^2. значит, это можно раскрыть как выражение (x-y), возведенное в квадрат, то есть, умножить это выражение на такое же. получается (x-y)(x-y). проводим остальные действия: выносим общие множители выражений за скобки и превращаем вторую дробь в обратную. в итоге получаются сократимые выражения, состоящие из множителей. (x+2y) сокращается в числителе первой дроби и в знаменателе второй. (x-y) сокращается в знаменателе первой дроби и в числителе второй. далее просто умножаем оставшиеся выражения на множители, которые выносили ранее. ответ:
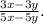
вывод. применение формул сокращенного умножения - их нужно закрывать или раскрывать в зависимости от того, что требуется в примере.
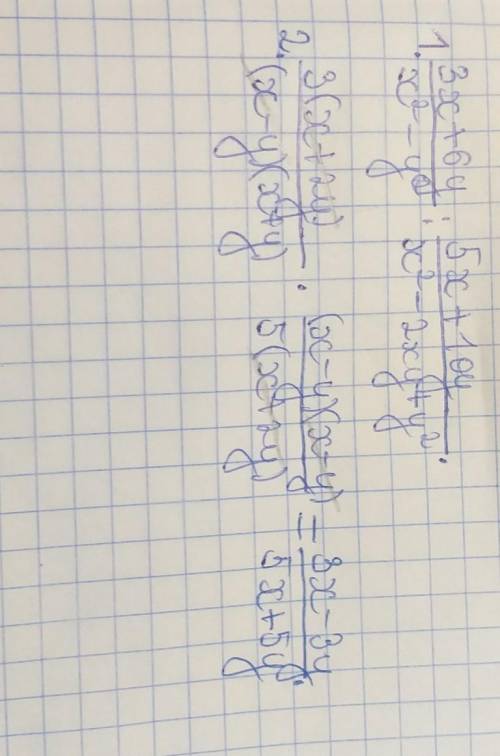
вот все расписано, только там сбоку иногда написано подробно, как вычислять, (ну это если ты не знаешь) удачи, хороших оценок