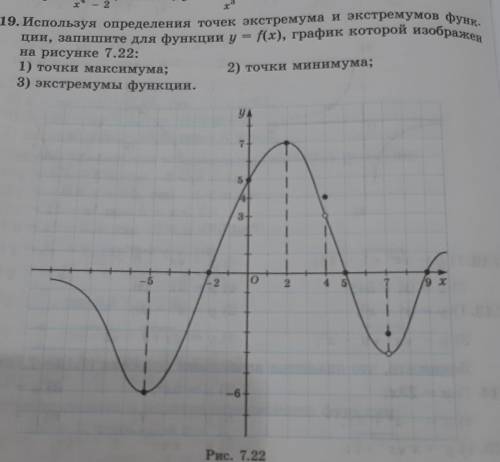
1) Точки максимума:
При х = 2, fmax = 7. Всего одна точка максимума.
2) Точки минимума:
При х = -5, fmin = -6. (При х=7, fmin = - 4, но здесь нет значения функции, так как очка выколотая). Всего одна точка минимума.
3) Точки экстремума:
Это все x-ы при которых есть минимум или максимум.
Их у нас 2. Уже говоролось ранее.
Это диофантово уравнение первой степени.
НОД (5,3) = 1 - уравнение имеет множество решений.
Оно описывается, соответственно, следующей системой двух кравнений:
х = 1 - 3n
y = 2+5n, где n - целое число.
Чтобы найти частные решения, нужно вместо n в данную систему подставлять по очереди 1, 2, 3, 4, 5 и т.д.
При n = 1 x = 1-3 = -2, y = 2+5 = 7. Пара чисел -2 и 7 является частным решением уравнения в целых числах.
При n = 2 x = 1 - 3*2 = 1 - 6 = -5, y = 2+5*2 = 2+10 = 12. Пара чисел (-5) и 12 является частным решением данного уравнения в целых числах.
Таким образом, подставляя вместо n любое целое число, вы найдете несколько частных решений.
1. точки: 5, 2
2. точки: 4,7
3. -5,-2,5,9