При имеющихся исходных данным возможно 2 ответа:
1) b₁ = 6; q = 1/4;
1) b₁ = -6; q = -1/4;
Объяснение:
Член геометрической прогрессии с номером n вычисляется по формуле
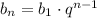
b₄ - b₂ = b₁ · q³ - b₁· q = b₁q(q² - 1)
b₆ - b₄ = b₁ · q⁵ - b₁· q³ = b₁q³(q² - 1)
По условию
b₁q(q² - 1) = -45/32 (1)
b₁q³(q² - 1) = -45/512 (2)
Преобразуем выражение (2)
b₁q³(q² - 1) = b₁q(q² - 1) · q²
В численном виде это можно записать как
-45/512 = -45/32 · q²
Откуда
q² = -45/512 : (-45/32)
q² = 1/16
q = ±1/4
Подставим q = 1/4 в выражение (1)
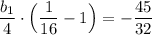
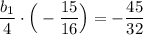
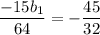
0.5b₁ = 3
b₁ = 6
Подставим q = -1/4 в выражение (1)
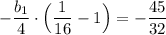
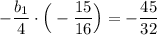

0.5b₁ = -3
b₁ = -6
Проверка:
1) b₁ = 6; q = 1/4
b₂ = 6 · 1/4 = 3/2
b₄ = 6 · 1/64 = 3/32
b₄ - b₂ = 3/32 - 3/2 = -45/32
b₆ = 6 · 1/1024 = 3/512
b₆ - b₄ = 3/512 - 3/32 = -45/512
2) b₁ = -6; q = -1/4
b₂ = -6 · (-1/4) = 3/2
b₄ = -6 · (-1/64) = 3/32
b₄ - b₂ = 3/32 - 3/2 = -45/32
b₆ = -6 · (-1/1024) = 3/512
b₆ - b₄ = 3/512 - 3/32 = -45/512
х=3+у
3(3+у)+у=5
9+3у+у=5
4у=-4
у=-1
Подставим найденное значение у в выраженное нами значение х:
х=3+у=3+(-1)=3-1=2
Проверим верность вычислений: 2-(-1)=2+1=3 - верно.
3*2+(-1)=6-1=5 - верно.
х=2, у=-1.
Б) Выразим у из первого уравнения системы и подставим во второе:
у=4-х²
2*(4-х²)-х=7
8-2х²-х=7
2х²+х-1=0
Д=1+8=9
х1=(-1+3):4=1/2
х2=(-1-3):4=-1
у=4-х²
При х1=1/2, у1=4-1/4=3 целых 3/4
При х2=-1, у2=4-(-1)²=4-1=3
х1=1/2, у1=3 целых 3/4; х2=-1, у2=3.
2.Подставим нашу точку (4;-2) в данные уравнения. Если в обоих уравнениях получится тождество, то эта пара чисел является решением системы, в противном случае-нет. На первом месте всегда стоит х, а на втором - у (если не оговорено в условиях другое).
Подставляем:
4+(-2)=2
4-2=2
2=2 - верно
4=-2, но 4≠-2. Второе условие не соответствует - пара чисел (4;-2) - не является решением для данной системы уравнений.