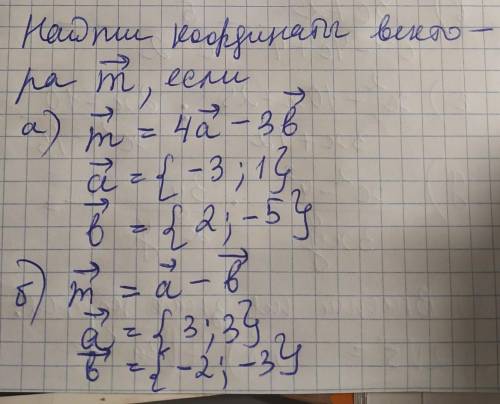
а и простите тел глюканул это ГЕОМЕТРИЯ

👇

Ответ:

egn96637

21.03.2022

$a)\vec{m}=\{-18;19\}\\b)\vec{m}=\{5;6\}$

Объяснение:

$a)\\\vec{m}=4\vec{a}-3\vec{b}\\\vec{a}=\{-3;1\} \Rightarrow 4\vec{a}=\{-12;4\}\\\vec{b}=\{2;-5\} \Rightarrow -3\vec{b}=\{-6;15\}\\\vec{m}=4\vec{a}-3\vec{b}=\{-12;4\}+\{-6;15\}=\{-12-6;4+15\}=\{-18;19\}$

$b)\\\vec{m}=\vec{a}-\vec{b}\\\vec{a}=\{3;3\}\\\vec{b}=\{-2;-3\} \Rightarrow -\vec{b}=\{2;3\}\\\vec{m}=\vec{a}-\vec{b}=\{3;3\}+\{2;3\}=\{2+3;3+3\}=\{5;6\}$

4,4(8 оценок)

Открыть все ответы

Ответ:

mariaalimardonova

21.03.2022

из условия задачи: 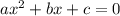$ax^{2}+bx+c=0$

решим систему уравнений, где в одном поменяем a и b, а в другом b и c.

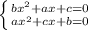
$\left \{ {{bx^{2}+ax+c=0} \atop {ax^{2}+cx+b=0}} \right.$

выразим дискриминант в обоих уравнениях и приравняем к 0, т.к. корень должен быть 1.

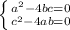
$\left \{ {{a^{2}-4bc=0} \atop {c^{2}-4ab=0}} \right.$

выразим 4b из первого уравнения и подставим во второе:

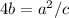
$4b=a^{2}/c$

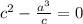
$c^{2}-\frac{a^{3}}{c} =0$

т.к. 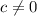$c \neq 0$

тогда 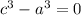$c^{3}-a^{3}=0$

$c^{3}=a^{3}$

c=a

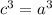
подставим в выражение, где твыразили 4b

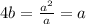
$4b=\frac{a^{2}}{a} = a$

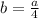
$b=\frac{a}{4}$

подставим все получившиеся коэффициенты в первое уравнеие:

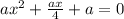
$ax^{2}+\frac{ax}{4} +a=0$

выразим дискриминант:

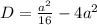
$D = \frac{a^{2}}{16} -4a^{2}$

видно, что дискриминант получится отрицательным, следовательно у данного трехчлена решений нет.

ответ: корней нет

4,5(19 оценок)

Ответ:

dashko4etckowa

21.03.2022

От речного порта А в порт В теплоход по течению проплывает за 3 суток, а против течения - за 7 суток. За сколько дней проплывет это расстояние плот?

Решение. Пусть собственная скорость теплохода равна х км\сутки, а скорость течения реки (скорость плота) y км\сутки, тогда скорость теплохода по течению реки равна км\сутки, против течения км\сутки. При равномерном движение расстояние=время*скорость.

По условию задачи составляем уравнение: 7(x-y)=3(x+y) (расстояние АВ)

7x-7y=3x+3y;

7x-3x=7y+3y;

4x=10y;

x=10y/4;

x=2.5y

Расстояние АВ=7*(x-y)=7*(2.5y-y)=7*1.5y=10.5y км

Скорость плота y км\сутки

Значит плот проплывет расстояние АВ за 10.5y/y=10.5 суток

ответ: за 10.5 суток

4,4(49 оценок)

Это интересно: