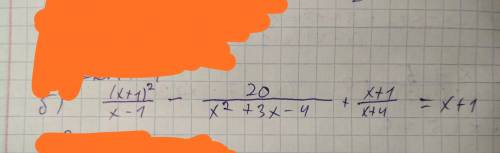
1. S1 совпадает с первым членом прогрессии:
Sn = 6n - n^2;
a1 = S1 = 6 * 1 - 1^2 = 6 - 1 = 5.
2. S2 - сумма первых двух членов прогрессии:
S2 = 6 * 2 - 2^2 = 12 - 4 = 8;
a1 + a2 = S2;
a2 = S2 - a1 = 8 - 5 = 3.
3. Разность прогрессии:
d = a2 - a1 = 3 - 5 = -2.
4. 6-й член вычислим по формуле для n-ого члена арифметической прогрессии:
an = a1 + (n - 1)d;
a6 = 5 + 5 * (-2) = 5 - 10 = -5.
5. Проверим сумму первых n членов прогрессии по формуле:
Sn = (2a1 + (n - 1)d)n/2;
Sn = (2 * 5 + (n - 1) * (-2))n/2 = (10 - 2(n - 1))n/2 = (10 - 2n + 2)n/2 = (12 - 2n)n/2 = (6 - n)n = 6n - n^2.
Объяснение:
ответ: -5.
Два велосипеда одновременно отъехали от общего старта велотрека в противоположных направлениях и встретились через 24 с. За какое время проедет один круг велотрека первый велосипедист, если второй преодолевает это же круг за 40 с?
Обозначим длину велотрека S м
(велотрек- это движение по кольцу- или по окружности)
Скорость первого х м/с, скорость второго у м/с
Если велосипедисты выехали в противоположных направлениях то с другой стороны они едут навтречу друг другу.
Значит скорость сближения х+у
и тогда (х+у)*24=S
второй преодолевает круг за 40 с, значит его скорость у=S/40
заменим в первом уравнении у=S/40
(x+S/40)*24=S
x+S/40=S/24
X=S/24-S/40=(5S-3S)/120=2S/120=S/60
но тогда x*60=S
а значит первый проедет трассу за 60с
Объяснение:
x * x + 3x - 4 имеет 2 корня: 1 и -4
Тогда приведем к общему знаменателю всё: (x-1) * (x + 4)
((x + 1) * (x + 1) * (x + 4) - 20 + (x + 1) * (x - 1)) / ((x - 1) * (x + 4)) = x + 1
умножим на (x - 1) * (x + 4)
((x + 1) * (x + 1) * (x + 4) - 20 + (x + 1) * (x - 1)) = (x + 1) * (x - 1) * (x + 4)
раскроем скобки:
x^3 + 6x^2+9x+4 - 20 + x^2 - 1 = x^3+4x^2-x-4
3x^2+10x-13 = 0
D = 10 * 10 + 4 * 13 * 3 = 100 + 12 * 13 = 100 + 156 = 256 = 16 * 16
x1, x2 = (-10 +- 16) / (2 * 3) = (-10 +- 16) / 6 = 1; -(4 + 1/3) можно записать как:
1 и -26/6