ответ:Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные (иногда натуральные или рациональные) наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.
Современной постановкой диофантовых задач мы обязаны французскому математику Ферма. Именно он поставил перед европейскими математиками во о решении неопределённых уравнений только в целых числах. Наиболее известное уравнение в целых числах – великая теорема Ферма: уравнение
xn + yn = zn
не имеет ненулевых рациональных решений для всех натуральных n > 2.
Теоретический интерес к уравнениям в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел.
В 1970 году ленинградский математик Юрий Владимирович Матиясевич доказал, что общего позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения, не существует и быть не может. Поэтому следует для разных типов уравнений выбирать собственные методы решения.
При решении уравнений в целых и натуральных числах можно условно выделить следующие методы перебора вариантов;
применение алгоритма Евклида;
представление чисел в виде непрерывных (цепных) дробей;
разложения на множители;
решение уравнений в целых числах как квадратных (или иных) относительно какой-либо переменной;
метод остатков;
метод бесконечного спуска.
Объяснение:
2)Подставим полученное выражение вместо х во второе уравнение системы: (5 - 3у) у — 2.
3)Решим полученное уравнение:
4) Подставим поочередно каждое из найденных значений у в формулу х = 5 - Зу. Если то
5) Пары (2; 1) и решения заданной системы уравнений.
Вычтем второе уравнение системы из ее первого уравнения:
В результате алгебраического сложения двух уравнений исходной системы получилось уравнение, более простое, чем первое и второе уравнения заданной системы. Этим более простым уравнением мы имеем право заменить любое уравнение заданной системы, например второе. Тогда заданная система уравнений заменится более простой системой:
Эту систему можно решить методом подстановки. Из второго уравнения находим Подставив это выражение вместо у в первое уравнение системы, получим
Осталось подставить найденные значения х в формулу
Если х = 2, то
Таким образом, мы нашли два решения системы:
0
Объяснение:
Найдём экстремумы функции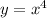
:
Найдем производную: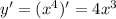
Найдем корни уравнения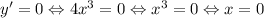
То есть в точке 0 функция имеет глобальный минимум.
Так как функция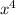
в точке 0 имеет глобальный минимум: