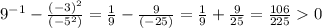Для вынесения множителя из под знака корня в данном случае нужно возвести множитель в степень, обратную степени корня. В данном случае наш корень имеет степень 11, поэтому мы должны возвести множитель в степень 1/11. Получится:
2)
Аналогично предыдущему примеру, теперь степень корня равна 4, поэтому мы должны возвести множитель в степень 1/4. Получится:
3)
Здесь наш множитель - переменная "а". С тем же принципом, мы должны возвести переменную "а" в степень 1/3:
Таким образом, мы вынесли множитель из-под знака корня в каждом из данных примеров, используя соответствующие степени.
Хорошо, я могу выступить в роли школьного учителя и помочь вам с решением этой задачи.
Чтобы найти квадраты выражений, мы должны возвести каждое из них в квадрат. Возведение в квадрат означает, что мы умножаем число на само себя. Давайте рассмотрим каждое выражение по отдельности:
1. a:
Чтобы найти квадрат выражения a, мы должны возвести его в квадрат:
a^2 = a * a
2. -4:
В этом случае у нас есть отрицательное число. Чтобы найти квадрат выражения -4, нам нужно умножить его на себя, сохраняя его знак:
(-4)^2 = -4 * -4 = 16
3. Зm:
Здесь у нас есть произведение числа 3 и переменной m. Чтобы найти квадрат этого выражения, мы должны умножить его на себя:
(3m)^2 = (3m) * (3m) = 9m^2
4. 2b:
В этом случае у нас есть произведение числа 2 и переменной b. Чтобы найти квадрат выражения 2b, мы должны умножить его на себя:
(2b)^2 = (2b) * (2b) = 4b^2
Итак, мы нашли квадраты каждого из данных выражений:
a^2 = a * a
(-4)^2 = 16
(3m)^2 = 9m^2
(2b)^2 = 4b^2
Используя эти формулы, вы сможете найти квадраты любых алгебраических выражений, помня о том, что возвести число или переменную в квадрат означает умножить его само на себя.
![\sqrt[11]{2 \ {}^{12} }](/tpl/images/3980/8684/8c53a.png)
1)
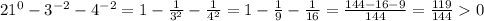
2)
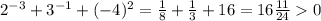
3)