y=x^2+16/x-16
y' = 2x+16*(-1/x^2)
y' = 0 -> 2x - 16/x^2=0
2x^3-16=0
x=2
y(2) = 4+8-16 = -4
y(3) = 9+16/3 - 16 = -5/3
y(6) = 36+16/6 - 16 = 20+16/6 = 68/3
Из этого следует,что наибольшее 68/3, а наименьшее -4
ответ: наибольшее 68/3, а наименьшее -4
3/4 (Это дробь).
Объяснение:
1.1. по определению:
(2−x)−1=12−x.
1.2. Рассмотрим важное тождество, которое часто используется на практике: (ab)−1=ba.
Значит: (2−x3x)−1=3x2−x.
1.3. Упростим выражение, которое находится в знаменателе дроби:
3−(2−x3x)−1=3−3x2−x=3\2−x−3x2−x=3(2−x)−3x2−x=6−3x−3x2−x=6−6x2−x.
1.4. Получим: 3x(2−x)−13−(2−x3x)−1=3x2−x6−6x2−x=3x2−x:6−6x2−x=3x2−x⋅2−x6−6x=3x(2−x)(2−x)(6−6x)=3x6−6x.
2. Далее подставим вместо x=35:
3x6−6x=3⋅356−6⋅35=(3⋅35):(6−6⋅35)=3⋅35:6⋅5−6⋅35=95⋅512=9⋅55⋅12=34.
 часа.
часа.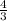 часа - 3 кг сплава
часа - 3 кг сплава кг сплава
кг сплава часа.
часа. часа - 3 кг сплава
часа - 3 кг сплава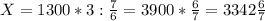 кг сплава
кг сплава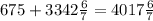 кг сплава
кг сплава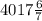 кг сплава.
кг сплава.
y наим = 3^2 + 16/3 - 16 = -5/3
y наиб = 6^2 + 16/6 - 16 = 68/3