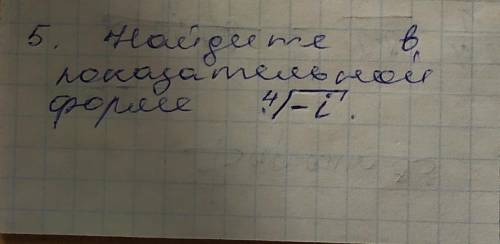
y=-x^2-4x - графиком функции является парабола, ветви направлены вниз
m=-b/2a = 4/2 = -2
y=-(-2)^2+4*2=4
(-2;4) - координаты вершины параболы
y=4+x - прямая, проходящая через точки (0;4), (-4;0)
Знайдемо обмежені лінії
\begin{gathered}-x^2-4x=4+x\\ x^2+5x+4=0\end{gathered}−x2−4x=4+xx2+5x+4=0
За т. Вієта: x_1=-1;\,\,\,\, x_2=-4x1=−1;x2=−4
Знайдемо площу фігури
\begin{gathered}\displaystyle \int\limits^{-1}_{-4} {(-x^2-4x-(4+x))} \, dx = \int\limits^{-1}_{-4} {(-x^2-5x-4)} \, dx =\\ \\ \\ =\bigg(- \frac{x^3}{3} - \frac{5x^2}{2}-4x\bigg)\bigg|^{-1}_{-4}= \frac{1}{3} - \frac{5}{2} +4- \frac{4^3}{3} + \frac{5\cdot4^2}{2} -16=4.5\end{gathered}−4∫−1(−x2−4x−(4+x))dx=−4∫−1(−x2−5x−4)dx==(−3x3−25x2−4x)∣∣∣∣∣−4−1=31−25+4−343+25⋅42−16=4.5
Объяснение:
Это
3)x=
4)x=
Объяснение:
3)
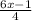 -
-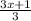 =
=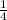
Умножаем обе части():
3(6x-1)-4(3x+1)=3
Распределить 3 и 4 через скобки:
18x-3-4(3x+1)=3
18x-3- 12x - 4=3
Привести подобные члены:
6x-3-4=3
6x-7=3
Переносим постоянную(-7) в правую часть и сменяем ее знак:
6x=3+7
Вычисляем:
6x=10
Разделим обе стороны на 6:
x=
4)
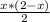 +
+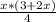 = 1
= 1
Раскрываем скобки:
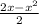 +
+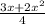 = 1
= 1
Умножаем обе части уравнения на 4:
2(2x- )+3x+2
)+3x+2
Распределяем 2 через скобки(2(2x- )):
)):
4x-2 +3x+2
+3x+2
Поскольку сумма двух противоположных величин равна нулю, надо удалить их из выражения(-2 и 2
и 2
4x+3x=4
7x=4
Разделить обе стороны на 7:
x=
Надеюсь
:)
Объяснение: