Пусть х производительность мастера, а y-ученика, тогда за 1 час мастер выполнит 1\х, а ученик 1\у, вместе за один час они выполнят 1\4. Получим уравнение: 1\х +1\у =1\4. х\2 – это время, которое потратит мастер на половину всей работы, а у\2 – время ученика, вместе они справятся за 9 часов. Получим уравнение: х\2 + у\2 = 9.
Составим и решим систему уравнений:
Решим 2-е уравнение системы: ОДЗ: y≠0 и y≠18 4y+72-4y-18+y²=0 y²-18y+72=0 D=b²-4ac=(-18)²4*72=324-288=36=6² *Разумно будет предположить, что мастер выполняет работу быстрей.
А) 1) f(-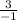 1) = -3
1) = -3
2) f ' (x) =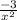
f ' (-1) =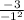 = -3
= -3
3) y= -3 - 3(x+1) = -3 -3x-3 = -3x -6
1) f(-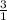 1) = 3
1) = 3
2) f ' (x) =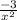
f ' (1) =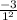 = -3
= -3
3) y = 3 - 3(x -1) = 3 - 3x + 3 = - 3x + 6
б) 1) f(0) = 2*0 - 0 = 0
2) f'(x) = (2x)' -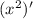 = 2 - 2x
= 2 - 2x
f'(0) = 2 - 2* 0 = 2
3) y = 2x
1) f(2) = 2*2 - 2^{2} = 0
2) f'(x) = (2x)' -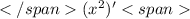 = 2 - 2x
= 2 - 2x
f'(2) = 2-2*2 = -2
3) y = -2(x-2) = -2x+4