Решите методом интервалов неравенство (71–73): 71. 1) (x + 2)(х – 7) > 0;
2) (х + 5)(х – 8) < 0;
3) (х-2)(х+
(х-2)(х + ) 0;
4) (х + 5) x-з) - о.
72. 1) х2 + 5x > 0; 2) х2 - 9x > 0;
3) 2x2-x < 0;
4) х2 + 3x < 0; 5) х2 + x — 12 < 0; 6) х2 - 2х - 3 > 0.
73. 1) х2 - 16x < 0;
2) 4x - x > 0;
3) (x2 - 1)(х + 3) < 0;
4) (x? - 4)(х - 5) > 0.


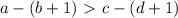
√(22/3) √ (17/2) √ (8/3) √(19/5)
например вот так
возведем их в квадрат
(22/3) (17/2) (8/3) (19/5)
приводим к наименьшему общему знаменателю (30)
220/30 255/30 80/30 57/30
и располагаем в порядке возрастания
57/30 80/30 220/30 255/30 ⇒255/30 =17/2 ⇒√(17/2 ) -наибольшее.
или так...
возведем их в квадрат и выделим целую часть
(22/3)=7+1/3 (17/2)=8+1/2 (8/3)=2+2/3 (19/5)=3+4/5 ⇒
(17/2)=8+1/2 - наибольшее среди (22/3), (17/2), (8/3), (19/5),
⇒√ (17/2) - наибольшее среди √(22/3), √ (17/2), √(8/3) , √(19/5).