Точки построения графика: (0;0), (±1; ±1), (±2; ±8). График является нечетной.
Подставим координаты точки A(-5;125) в график уравнения, получим
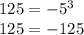
Поскольку равенство не верно, то график функции y = x³ не проходит через точку A(-5;125), т.е. точка не принадлежит графику y = x³
Подставим теперь координаты точки B(4;64), получим
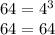
Поскольку равенство тождественно выполняется, то точка B принадлежит графику функции y = x³.
Подставим координаты точки C(-3;-27), имеем
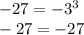
Раз равенство тождественно выполняется, то точка C(-3;-27) принадлежит графику функции y = x³
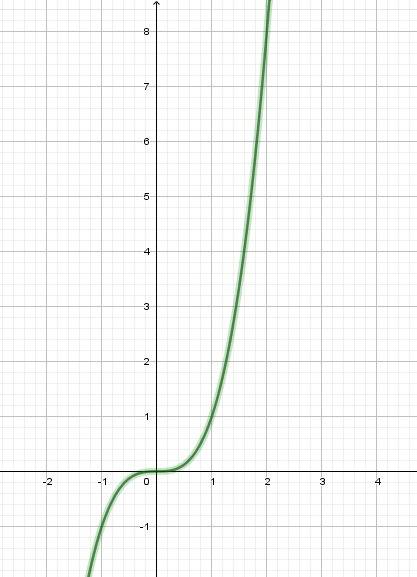
Уравнение касательной y = f ’(x0) · (x − x0) + f (x0)
Здесь f ’(x0) — значение производной в точке x0, а f (x0) — значение самой функции.
Значение функции в точке х = 2:
f(2) = 2-3*2² = 2-12 = -10.
Производная функции равна f'(x) = 1-6x.
В точке Хо = 2 её значение f'(2) = 1-6*2 = -11.
Уравнение касательной: у = -11(х-2)-10 или, раскрыв скобки,
у = -11х+22-10 = -11х+12.
B2) Даны уравнения функции y=0,5x^4-x и касательной к её графику
y=-(3/4)x-(3/32).
Відповідь:
ПАГМКТЩТАСМИ
Пояснення: