Решить уравнение: |x+1|-|x-2|+|3x+6|=5.
3|x+2| +|x+1|- |x-2| =5.
- - - + - - + + - + + +
(-2) (-1 ) (2)
a) { x < -2 ; -(3x -6) -(x +1) +(x -2)=5.⇔ { x < -2 ; x = -14/3. ⇒ x = -14/3.
б) { -2 ≤ x< - 1 ; 3x+6 -(x+1) +(x -2)=5.⇔ { -2 ≤ x<- 1 ; x = 2/3.⇒ x ∈∅.
в) { - 1 ≤ x< 2 ; 3x+6 +(x +1) +(x -2)=5.⇔ {-1 ≤ x< 2 ; x = 0. ⇒ x = 0.
д) { x≥ 2 ; 3x+6 +(x +1) - (x -2)=5.⇔ {1 ≤ x< 2 ; x = - 4/3. ⇒ x ∈∅.
ответ: - 14/3 ; 0 .
Условие. Y²+xy-4x-9y+20=0 ; y=ax+1 ; x>2
найти все значения а, при которых графики имеют одну общую точку(в нашем случае (ax+1)² + x(ax+1) -4x - 9(ax+1)+20=0 имеет единственное решение).
Подставим у = (ax+1)² в уравнение у²+xy-4x-9y+20=0, получим
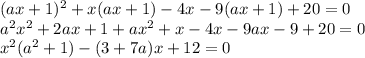
Найдем дискриминант квадратного уравнения относительно x
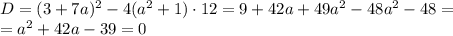
Получим 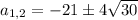
Если подставить 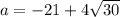 , т.е. имеется квадратное уравнение
, т.е. имеется квадратное уравнение  , у которого корень
, у которого корень
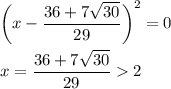
Если подставить  , т.е. имеется квадратное уравнение
, т.е. имеется квадратное уравнение 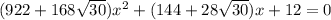 , у которого корень
, у которого корень
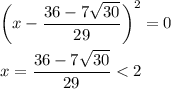
ответ: 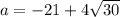
sin^2a(1/cos^2a -1)/cos^2a(1/sin^2a-1)={sin^2acos^2a/(1-cos^2a)}/{cos^2asin^2a/(1-sin^2a)}=
=cos^2a/sin^2a=ctg^2a
2) условие не совсем верное т.к. синус во вторй четверти положительный, а у тебя написано отрицательный.
cosa=-V(1-0.64)=-V0.36=-0.6
tga=sina/cosa=0.8/-0.6=-8/6=-4/3
ctga=1/tga=-3/4