Сторона данного треугольника а(3) равна Р:3=6√3:3=2√3 дм
Формула радиуса окружности, описанной около правильного треугольника:
R=a/√3 =>
R=2√3:√3=2 дм
Формула стороны правильного многоугольника через радиус вписанной окружности:
а(n)=2r•tg(180°:n), где r – радиус вписанной окружности, n – число сторон,
Для правильного шестиугольника tg(180°:n)=tg30°=1/√3
a₆=2•2•1/√3=4/√3
P=6•4/√3=8√3 дм
—————
Как вариант: Правильный шестиугольник состоит из 6 равных правильных треугольников.
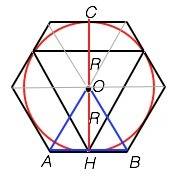
На рисунке приложения ОН - радиус описанной около правильного треугольника окружности и в то же время высота одного из 6 правильных треугольников, все углы которого 60°; АВ - сторона шестиугольника. Задача решается с т.Пифагора.
О чем бы разговор ни был, он всегда умел поддержать его: шла ли речь о лошадином заводе, он говорил и о лошадином заводе; говорили ли о хороших собаках, и здесь он сообщал очень дельные замечания; трактовали ли касательно следствия, произведенного казенною палатою, - он показал, что ему небезызвестны и судейские проделки; было ли рассуждение о бильярдной игре - и в бильярдной игре не давал он промаха; говорили ли о добродетели, и о добродетели рассуждал он очень хорошо, даже со слезами на глазах; об выделке горячего вина, и в горячем вине знал он прок; о таможенных надсмотрщиках и чиновниках, и о них он судил так, как будто бы сам был и чиновником и надсмотрщиком.