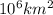Решение a) Пусть ε > 0. Требуется поэтому ε найти такое δ > 0, чтобы из условия 0 < |x − x0| < δ, т.е. из 0 < |x - 0| < δ вытекало бы неравенство |f(x) − A| < ε, т.е. |3x - 2 − (- 2)| < ε. Последнее неравенство приводится к виду |3(x )| < ε, т.е. |x | < (1/3)* ε. Отсюда следует, что если взять δ = ε/3 , то неравенство 0 < |x | < δ будет автоматически влечь за собой неравенство |3x - 2 − (- 2)| < ε. По определению это и означает, что lim x→ −2 (3x - 2) = −2
1) Область определения: x ∈ (-∞; ∞). 2) Четность-нечетность: Т.к. и , то функция является функцией общего вида. 3) Точки пересечения с Ox. Решим исходное уравнение при y = 0. (метод решения: Виета-Кардано) Получим один корень: x = 0.148 - абсцисса точки пересечения графка с осью Ox. Координаты точки: (0.148; 0)
Точка пересечения с Oy. Найдем y, подставив в уравнение x = 0. Получим: y = -5. Координаты точки: (0, -5).
4) Так как функция кубическая, то точек экстремума не имеет.
5) Первая производная.
2. Вторая производная. Находим корни уравнения. Для этого полученную функцию приравняем к нулю. Откуда точка перегиба: x = 5/3
и 
, то функция является функцией общего вида.
469 квадратных км
ибо 1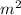
= 