Question

X^ log2x+2=8 , умоляю, ! икс в степени((логарифм числа икс по основанию 2)+2) =8

Answer 1

$x^{log_2 x+2}=8;\\ x0;\\ (log_2 x+2)*log_2 x=log_2 8;\\ log^2_2 x+2log_2 x=log_2 2^3;\\ log^2_2 x+2log_2 x-3=0;\\ (log_2 x+3)*(log_2 x-1)=0;\\ 1. log_2 x=-3;\\ x_1=2^{-3}=\frac{1}{2^3}=\frac{1}{8}=0.125;\\ 2. log_2 x=1;\\ x_2=2^1=2;$

Answer 2

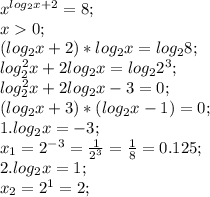
Если расписать 8 как 2^3, то х=2, и (логарифм х по основанию 2)+2=3

во втором уравнении х=2, т.е. єто и есть решение

Как-то так... 

ОК. Через логарифмирование.

Напишите логарифм по основанию 2 перед х в степени (...) и такой же логарифм по сонованию 2 перед 8 (я бы написала, но здесь в формулах нет логарифмов).

Получится, исходя из свойств логарифма:

(log{2}x+2)(log{2}x)=3log{2}2

Для удобства написания обозначаю log{2}x через t, т.е. (t+2)t=3

t^2+2t-3=0

t=(-2-4)/2=-3 - не подходит, т.к. меньше 0.

t=(-2+4)/2=1

log{2}x=1, значит х=2