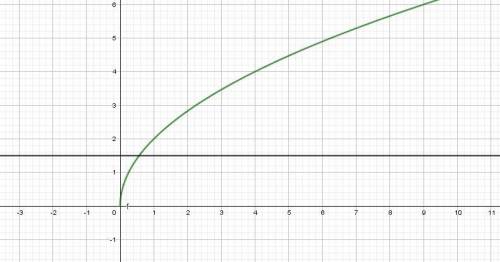
1) Построим графики функций 
и прямую параллельную оси ОХ 
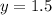
Графики пересекаются в точке (0.5625; 1.5), где x = 0.5625 - корень данного уравнения
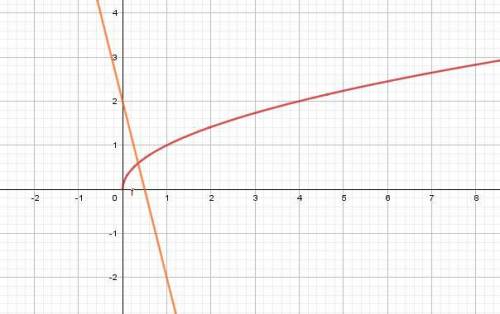
2) Построим график функции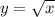 
и прямую 
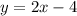проходящую через точки (0;-4), (2;0). Отсюда абсцисса точки пересечения двух графиков 
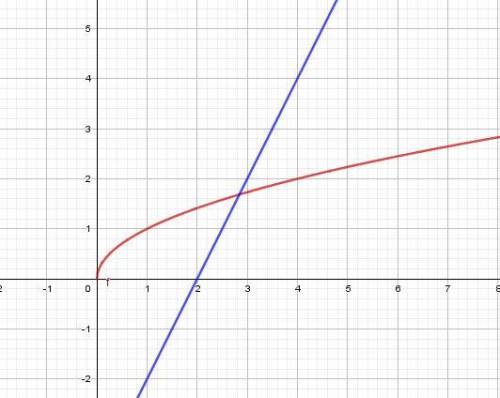
3) Построим график функции y = √x и прямую y = 2 - 4x, проходящую через точки (0;2), (1;-2). Абсцисса точки пересечения двух графиков равна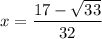 
4) Построим график функции y = 0.4√x и прямую y = 1 - 2x, проходящую через точки (0;1), (1;-1). Абсцисса точки пересечения двух графиков равна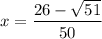 
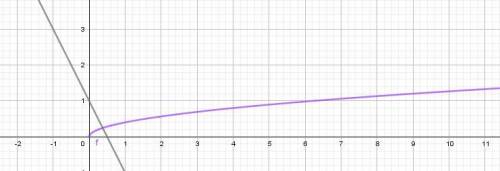
1) Построим графики функций и прямую параллельную оси ОХ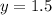
Графики пересекаются в точке (0.5625; 1.5), где x = 0.5625 - корень данного уравнения
2) Построим график функции 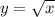и прямую 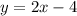проходящую через точки (0;-4), (2;0). Отсюда абсцисса точки пересечения двух графиков
3) Построим график функции y = √x и прямую y = 2 - 4x, проходящую через точки (0;2), (1;-2). Абсцисса точки пересечения двух графиков равна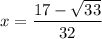
4) Построим график функции y = 0.4√x и прямую y = 1 - 2x, проходящую через точки (0;1), (1;-1). Абсцисса точки пересечения двух графиков равна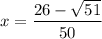
В решении.
Объяснение:
х - вес 1 гири.
у - вес 1 гантели.
По условию задачи система уравнений:
4х + 5у = 89
3х - 7у = 13
Разделить первое уравнение на 4 для упрощения:
х + 1,25у = 22,25
3х - 7у = 13
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х = 22,25 - 1,25у
3(22,25 - 1,25у) - 7у = 13
66,75 - 3,75у - 7у =13
-10,75у = 13 - 66,75
-10,75у = - 53,75
у = -53,75/-10,75
у = 5 (кг) - вес 1 гантели.
х = 22,25 - 1,25у
х = 22,25 - 1,25 * 5
х = 22,25 - 6,25
х = 16 (кг) - вес 1 гири.
Проверка:
4*16 + 5*5 = 64+25=89
3*16 - 7*5 = 48-35=13, верно.