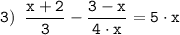
Объяснение:
Целым уравнением с одной переменной называется уравнение, левая и правая части которого - целые выражения. Отличие целого уравнения от дробно-рационального заключается в том, что областью определения целого уравнения является множество всех действительных чисел. Выполнив над целыми уравнениями равносильные преобразования можно получит уравнение вида P(x) = 0, где P(x) – многочлен в стандартном виде.
1) 3-34·(3·x-10)·(6·x+80)=7·x
3-34·(18·x²+240·x-60·x-800)=7·x
3-34·(18·x²+180·x-800)-7·x=0
3-612·x²-6120·x+27200-7·x=0
612·x²+6127·x-27203=0
P₂(x)=612·x²+6127·x-27203.
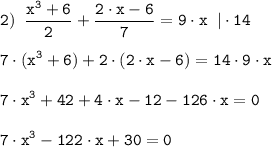
P₃(x)=7·x³-122·x+30
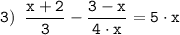
Так как в знаменателе присутствует неизвестная x, то x≠0, то есть областью определения целого уравнения не является множество всех действительных чисел.
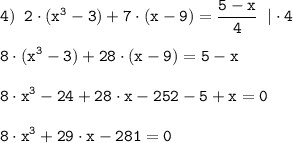
P₃(x)=8·x³+29·x-281.
3а+(2а-10)-(12+2а)=3a+2a-10-12-2a=3a-22
(6х-8)-5х-(14-9x)=6x-8-5x-14+9x=10х-22
3в-(в-(2в-4))=3в-(в-2в+4)=3в-в+2в-4=4в-4
3х-((y-x)+3y)=3х-(у-х+3у)=3х-у+х-3у=4х-4у