7–10. Два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней. Решаем уравнения, находим корни уравнения и сравниваем ответы.
7. 1) 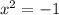
число в корне не может равняться отрицательному числу, корней уравнения нет.
2) 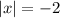
число в модуле не может равняться отрицательному числу, корней уравнения нет.
=> уравнения равносильные.
8. 1) 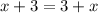
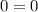
корней уравнения нет.
2) 
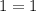
корней уравнения нет.
=> уравнения равносильные.
9. 1) 
ОДЗ: 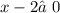 ,
, 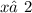 ;
;
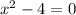
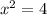
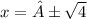
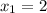 (не удовлетворяет ОДЗ),
(не удовлетворяет ОДЗ), 
ответ: 
2) 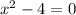
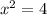
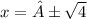
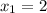 ,
, 
ответ:  ;
; 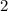
=> уравнения не равносильные.
10. 1) 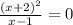
ОДЗ: 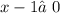 ,
, 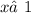 ;
;
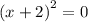
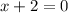

ответ: 
2) 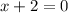

ответ: 
=> уравнения равносильные.

12–16. Необходимо найти сумму корней уравнения. Решаем уравнение, находим корни уравнения, складываем их. Если уравнение имеет один корень, то суммой (ответом) будет значение корня уравнения.
12. 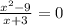
ОДЗ: 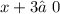 ,
,  ;
;
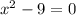


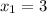 ,
,  (не удовлетворяет ОДЗ)
(не удовлетворяет ОДЗ)
ответ: 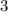
13. 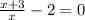
ОДЗ: 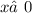 ;
;
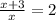
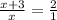
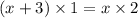
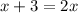
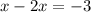
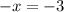
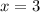
ответ: 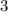
14. 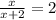
ОДЗ:  ,
,  ;
;
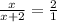
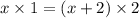

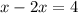


ответ: 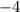
15. 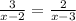
ОДЗ: 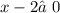 ,
, 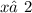 ,
, 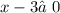 ,
,  ;
;
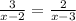
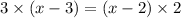
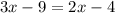
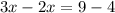
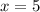
ответ: 
16. 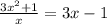
ОДЗ: 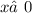 ;
;
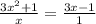
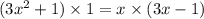
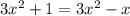
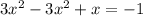

ответ: 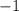
Функция y=f(x) – соответствие, при котором каждому числу x из множества D сопоставляется единственное число y из множества E.
x– аргумент функции, y – значение функции; D или D(f) – область определения функции; это совокупность всех значений x, для которых можно вычислить значение функции. E или E(f) – область значений функции; это совокупность всех значений, которые может принимать выражение f(x).
График функции y=f(x) – множество точек (x,y) на координатной плоскости, где x принимает все возможные значения из D(f), а y=f(x).
Четная функция: f(-x)=f(x) для всех ;
Нечетная функция: f(-x)=-f(x) для всех ;
График четной функции симметричен относительно оси OY. График нечетной функции симметричен относительно начала координат.
Надеюсь разберешь! Решение во вложении