Question

Исследовать знакопеременный ряд на абсолютную и условную сходимость

Answer 1

$\sum \limits _{n=1}^{\infty }\, a_{n}=\sum \limits _{n=1}^{\infty }\dfrac{cos\, 9^{n}}{(2n+3)!}\\\\\\\sum \limits _{n=1}^{\infty }\, |\, a_{n}\, |=\sum \limits _{n=1}^{\infty }\dfrac{|\, cos\, 9^{n}\, |}{(2n+3)!}\\\\\\\dfrac{|\, cos\, 9^{n}\, |}{(2n+3)!}\leq \dfrac{1}{(2n+3)!}\ \ \ ,\ \ \ \ \sum \limits _{n=1}^{\infty }b_{n}=\sum \limits _{n=1}^{\infty }\dfrac{1}{(2n+3)!}\ -\ sxoditsya\ ,\ tak\ kak$

$po\ priznaky\ Dalambera\\\\\lim\limits _{n \to \infty}\dfrac{b_{n+1}}{b_{n}}=\lim\limits _{n \to \infty}\dfrac{1}{(2n+5)!}:\dfrac{1}{(2n+3)!}=\lim\limits _{n \to \infty}\dfrac{(2n+3)!}{(2n+5)!}=\\\\\\=\lim\limits _{n \to \infty}\dfrac{(2n+3)!}{(2n+3)!\cdot (2n+4)(2n+5)} =\lim\limits _{n \to \infty}\dfrac{1}{(2n+4)(2n+5)}=0$

Сходится мажорантный ряд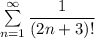   $\sum \limits _{n=1}^{\infty }\dfrac{1}{(2n+3)!}$   , значит по признаку сравнения сходится и минорантный ряд     $\sum \limits _{n=1}^{\infty }\dfrac{|cos\, 9^{n}|}{(2n+3)!}$   -  ряд,

составленный из абсолютных величин исходного ряда.

Из сходимости ряда из абсолютных величин следует  абсолютная

сходимость исходного ряда .