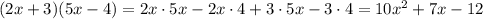
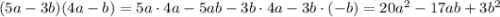
Объяснение:
1. Постройте график функции y=2x-1. По графику найдите: а) значения функции при значениях аргумента, равных -2;0;3; б)
значения аргумента, при которых значения функции равны 3;7; в) найдите точку пересечения данной прямой с прямой, заданной уравнением x=4
Функция у = 2х - 1 является линейной функцией, то есть графиком данной функции будет прямая. Для построения прямой достаточно двух точек.
х = 1; у = 2 * 1 - 1 = 1. Точка (1; 1).
х = 5; у = 2 * 5 - 1 = 9. Точка (5; 9).
Чертим координатную плоскость, ставим точки, проводим прямую.
а) Значения функции - это значение у, значение аргумента - это значение х. Находим точки -2, 0 и 3 на оси х, мысленно проводим вертикальную прямую и определяем координату у в точке на прямой.
х = -2; у = -5.
х = 0; у = -1.
х = 3; у = 5.
б) Находим точки 3 и 7 на оси у, мысленно проводим горизонтальную прямую, определяем координату х на прямой.
у = 3; х = 2, точка (3; 2).
у = 7; х = 4.
в) Прямая х = 4 - это вертикальная прямая, пересекающая ось х в точке 4. Чертим данную прямую, определяем координаты точки пересечения. Точка (4; 7)
1) f(x) = x^2 - 6x + 5
D(f) = R
1) Знайдемо проміжки монотоності:
f`(x) = 2x - 6 = 2(x - 3)
f`(x) = 0
2(x - 3) = 0
x = 3
(дивись малюнок)
f(x) спадає якщо х ∈ (-∞; 3) і зростає якщо х ∈ (3; +∞)
2) знайдемо точки екстремума.
х(min) = 3 ⇒ y(min) = 3² - 6 * 3 +5 = 9 - 18 + 5 = -4
точки max не існеє.
2) f(x) = x^4 - 2x^2
D(f) = R
1) Знайдемо проміжки монотоності:
f`(x) = 4x³ - 4х = 4х(x² - 1) = 4х(х - 1)(х + 1)
f`(x) = 0
4х(х - 1)(х + 1) = 0
х = 0, х = 1, х = -1
(дивись малюнок)
f(x) спадає якщо х ∈ (-∞; -1) і (0; 1);
зростає якщо х ∈ (-1; 0) і (1; +∞)
2) знайдемо точки екстремума.
х(min) = -1 ⇒ y(min) = (-1)⁴ - 2 * (-1)² = 1 - 2 = -1
х(min) = 1 ⇒ y(min) = 1⁴ - 2 * 1² = 1 - 2 = -1
х(max) = 0 ⇒ y(max) = 0⁴ - 2 * 0² = 0

Объяснение:
.......................