1. |x²-7|+12=0
|x²-7|=-12
x∈∅
Данное уравнение не имеет корней, т.к. модуль является неотрицательным числом.
2. Выделим полный квадрат:
x²-6x+8 = (x²-2x*3+3²) -3²+ 8 = (x-3)² -9 + 8 = (x-3)² -1
Разложим на множители x²-6x+8 = (x-x₁)(x-x₂)
По теореме Виета находим корни: х₁*х₂=8 и х₁+х₂=-6 => х₁=2 и х₂=4
x²-6x+8= (x-2)(x-4)
3. 3x²-6x+c=0, x₁=x₂
По условию, квадратное уравнение имеет равные корни, следовательно, дискриминант этого уравнения равен нулю.
Находим с:
D= (-6)²-4*3*c = 36-12c
36-12c = 0
12c = 36
c = 3
Вариант Б1:
1Дано:
АО=DO
<1=<2
Док-ть: тр. АОВ=тр. DOC
Доказательство:
1) <ВАО+<1 = 180° (смежные)
<CDO+<2 = 180° (смежные)
<ВАО = 180 - <1
<CDO = 180 - <2
Т.к. <1 и <2 равны (по усл.), то:
<BAO=<CDO
2) Рассмотрим тр-ки AOB и DOC:
<BAO=<CDO (доказано)
<BOA = <COD (вертик.)
AO=DO (по усл.)
Значит,
тр AOB = тр DOC
Доказано.
2Дано:
ABCD — четырехугольник
AD=BC, AB = CD
Доказать: <А = <С
Доказательство:
1) Доп. построение — диагональ BD
2) Рассм. тр-ки ABD и CBD:
AD = BC, AB = CD (по усл.)
BD — общая.
Значит,
тр ABD = тр CBD
3) В равных треугольниках все соответствующие элементы равны.
Значит,
<A = <C
<A = <CДоказано.
3Дано:
ABCD — четырёхугольник
BD, AC — диагонали.
тр ABC = тр CDA
Доказать: тр ABD = тр CDB
Доказательство:
1) Т. к. тр-ки ABC и CDA равны, то:
AD = BC
AB = CD
2) Рассмотрим тр-ки ABD и CDB:
AD = BC, AB = CD (док.)
BD — общая
Значит,
тр ABD = тр CDB
Доказано.
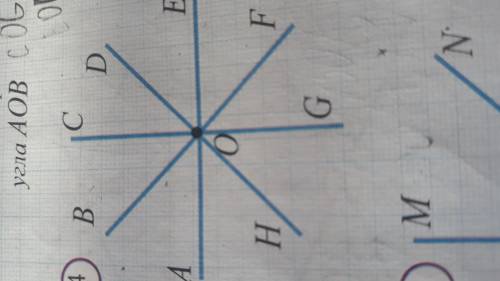
а)На рисунке 8 острых углов это:
углы AOB BOC COD DOE EOF FOG GOH HOA
б)На рисунке тупых углов это:
углы AOF BOG COH DOA COF DOG EOH BOE
На рисунке прямых углов это:
углы AOG AOC COE EOG DOF FOH HOB BOD
г)На рисунке развернутых углов это
углы AOE BOF COG DOH
Объяснение:
Прямые равны 90 градусам, острые меньше 90 градусов, тупые больше 90 градусов, развернутые равны 180 градусам