ответ: 24 см и 12 см.
Объяснение:
Пусть l - длина отрезка, соединяющего середины диагоналей трапеции. Этот отрезок лежит на средней линии трапеции и равен полуразности её оснований. Пусть a и b - основания трапеции, причём a>b, а c - длина средней линии трапеции. Так как по условию диагонали трапеции делят её среднюю линию на 3 равных части, то l=c/3. Отсюда c=3*l=3*6=18 см и, так как c=(a+b)/2, то мы получаем систему уравнений:
(a-b)/2=6
(a+b)/2=18
или:
a-b=12
a+b=36
Решая её, находим a=24 см и b=12 см.
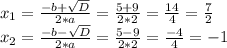
Объяснение:
Предыдущее мое решение было неверным, так как Вы неправильно указали формулировку уравнения.
Если уравнение имеет вид:
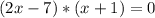
Мы имеем право перемножить обе скобки между собой, получим:
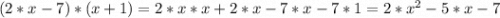
Теперь мы получили обычное квадратное уравнение:

Находим дискриминант:
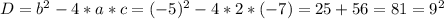
Тогда корни уравнения будут:
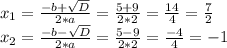
Это и будут корни нашего уравнения.
Можно было решить гораздо проще и приравнять каждую из скобок в произведении уравнения к нулю, и решать как два отдельных уравнения. Тот быстрее, потому что мы без нахождения дискриминанта сразу получаем два корня:
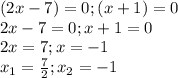
ровно d
надеюсь