
В двудольном графе, который содержит n вершин в одной доле и m вершин в другой, наибольшее количество рёбер будет тогда, когда каждая вершина из одной доли будет соединена с каждой вершиной в другой доле.
В этом случае количество ребёр будет равно n*m
В нашей задаче известно, что граф содержит 100 вершин.
Пусть количество вершин в одной доле равно n. Тогда в другой доле будет 100 - n вершин.
Количество ребёр тогда равно n(100 - n)
n(100 - n) = -n² + 100n
График полученного выражения - парабола, ветви которой направлены вниз (т.к. коэффициент при n² меньше 0)
Следовательно наибольшее значения будет в вершине данной параболы
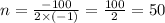
Тогда количество рёбер равно 50(100 - 50) = 2500
пусть х - деталей в час должен был по плану выполнять завод,
(x+20) - деталей в час должен по факту выполнял завод.
тогда 120/x-120/(x+20)=1
решаем 120(x+20)-120x=(x+20)x
120·20 =x²-20x x²+20x-120·20=0
x1=-10-√(100+120·20)<0
x2=-10+√(100+120·20)=-10+50=40
ответ: 40 деталей в час должен был по плану выпускать .
проверка дает положительный результат.