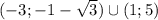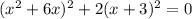
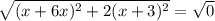
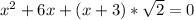
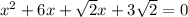
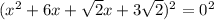
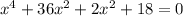
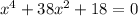
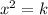
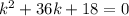
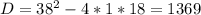
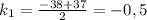
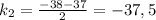
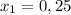
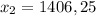
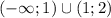
Объяснение:
Перенесём один из корней влево, а одну из семёрок — вправо следующим образом:
![7^{ax^2-2x}-7^{x^2-1}=\sqrt[7]{2x-ax^2}-\sqrt[7]{1-x^2} \\7^{ax^2-2x}-\sqrt[7]{2x-ax^2}=7^{x^2-1}-\sqrt[7]{1-x^2}\\7^{ax^2-2x}+\sqrt[7]{ax^2-2x} =7^{x^2-1}+\sqrt[7]{x^2-1}](/tpl/images/4771/4253/b4ecf.png)
Рассмотрим функцию ![f(x)=7^x+\sqrt[7]{x}](/tpl/images/4771/4253/5e929.png) . Она представляет собой сумму двух монотонно возрастающих функций (показательная и функция корня седьмой степени), следовательно она также монотонно возрастает. Значит, каждому аргументу соответствует ровно одно значение функции, то есть функция f(x) взаимно однозначна.
. Она представляет собой сумму двух монотонно возрастающих функций (показательная и функция корня седьмой степени), следовательно она также монотонно возрастает. Значит, каждому аргументу соответствует ровно одно значение функции, то есть функция f(x) взаимно однозначна.
Уравнение в таком случае принимает следующий вид:
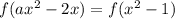
Поскольку каждому значению функции соответствует только одно значение аргумента, равенство значений функции можно свести к равенству её аргументов:
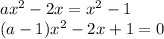
Если 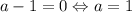 , то это линейное уравнение, имеющее не более одного корня, что не подходит.
, то это линейное уравнение, имеющее не более одного корня, что не подходит.
Если 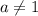 , то это квадратное уравнение. Оно имеет два корня при положительном дискриминанте:
, то это квадратное уравнение. Оно имеет два корня при положительном дискриминанте:
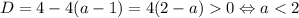
Учитывая, что 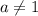 , получаем ответ
, получаем ответ 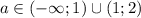
ОДЗ:
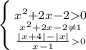
Решаем каждое неравенство:
 ⇒
⇒ 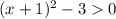 ⇒
⇒

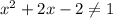 ⇒
⇒  ⇒
⇒ 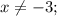
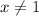

Подмодульные выражения обращаются в 0 в точках
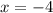 и
и 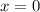
Это точки делят числовую прямую на три промежутка.
Раскрываем знак модуля на промежутках:
(-∞;-4]
|x+4|=-x-4
|x|=-x
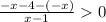 ⇒
⇒  ⇒ x < 1
⇒ x < 1
решение неравенства (-∞;-4]
(-4;0]
|x+4|=x+4
|x|=-x
 ⇒
⇒  ⇒ x < -2 или x > 1
⇒ x < -2 или x > 1
решение неравенства (-4;-2)
(0;+∞)
|x+4|=x+4
|x|=x
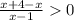 ⇒
⇒  ⇒ x > 1
⇒ x > 1
решение неравенства (1;+∞]
Объединяем ответы трех случаев:
 при
при 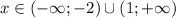
ОДЗ:

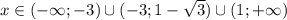
Решаем неравенство: 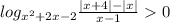
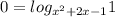
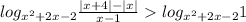
Два случая:
если основание логарифмической функции >1, то она возрастает и большему значению функции соответствует большее значение аргумента
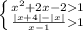 ⇒
⇒  ⇒
⇒ ![\left \{ {{x\in (-\infty;-3) \cup(1;+\infty)} \atop {x\in(-\infty;-4]\cup(1;5)}} \right.](/tpl/images/1360/8793/82812.png)
второе неравенство решаем на промежутках так:
(-∞;-4]
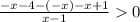 ⇒
⇒  ⇒
⇒ 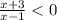 ⇒ (-3;-1)
⇒ (-3;-1)
не принадлежат (-∞;-4]
на (-4;0]
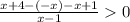 ⇒
⇒ 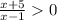 ⇒ x < -5 или x > 1
⇒ x < -5 или x > 1
не принадлежат (-4;0]
(0;+∞)
 ⇒
⇒ 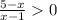 ⇒
⇒ 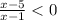 ⇒
⇒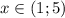
о т в е т этого случая 
если основание логарифмической функции 0 < a < 1, то она убывает и большему значению функции соответствует меньшее значение аргумента
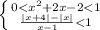 ⇒
⇒  ⇒
⇒ ![\left \{ {{x\in (-3;-1-\sqrt{3}) \cup(-1+\sqrt{3};1)} \atop {x\in(-\infty;-4]\cup(-4;0]\cup(5;+\infty)}} \right.](/tpl/images/1360/8793/ac205.png)
второе неравенство решаем на промежутках так:
(-∞;-4]
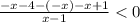 ⇒
⇒ 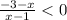 ⇒
⇒ 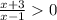 ⇒
⇒
(-∞;-3)U(1;+∞)
о т в е т. (-∞;-4]
на (-4;0]
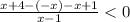 ⇒
⇒ 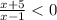 ⇒ -5 < x < 1
⇒ -5 < x < 1
о т в е т. (-4;0]
(0;+∞)
 ⇒
⇒ 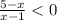 ⇒
⇒ 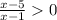 ⇒
⇒
о т в е т этого случая 
С учетом ОДЗ получаем окончательный ответ: