Объяснение:
Принимаем отремонтированное здание за единицу (1), а время, затраченное на ремонт этого здания за х. ⇒
Если бы работала только первая бригада, то ей потребовалось бы
(х+10) дней, если бы работала только вторая бригада, то ей потребовалось бы (х+20) дней, а если бы работала только третья бригада, то ей потребовалось бы 6*х дней. ⇒
Скорость выполнения работ первой бригадой равна 1/(х+10),
второй бригадой - 1/(х+20), третьей бригадой - 6х.
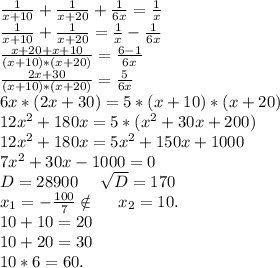
ответ: за 20 дней может выполнить задание первая бригада,
работая самостоятельно; за 30 дней может выполнить задание вторая бригада, работая самостоятельно; за 60 дней может выполнить задание третья бригада, работая самостоятельно.
1. а) a-b=0,04
а>b, т.к. только вычитая из большего числа меньшее, мы получаем положительное число.
б) a-b=-0,01
а<b, т.к. вычитая из меньшего числа большее мы будем всегда получать отрицательное число.
2. а) (x-3)² > x(x-6)
Воспользуемся формулой квадрата разности: (а-b)²=a²-2ab+b²
х²-2*3х+3² > x*x-6x
x²-6x+9 > x²-6x
x²-6x+9-x²+6x > 0
9>0
Неравенство верно, от х не зависит.
Вывод: неравенство (x-3)² > x(x-6) верно при любых значениях х.
б) (x+5)² > x(x+10)
х²+2*5*х+5² > x*x+10x
x²+10x+25 > x²+10x
x²+10x+25-x²-10x > 0
25 > 0
Неравенство верно, от х не зависит.
Вывод: неравенство (x+5)² > x(x+10) верно при любых значениях х.
1/x = 36+24+x/72*(x+24)
1/x = 60 = x/72*(x+24)
1/x = 60+x/72x + 1728
72x + 1728 = 60x + x²
x² - 12x - 1728 = 0
x1 = 48
x2 = -36