В решении.
Объяснение:
2. Чи належить графіку функції у = х² - х +1 точка:
1) А (0 ;-1)
2) В(0; 1)
3) С(2;0)
4) D(1;1)
5) Е(-2;6)
Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение. Если левая часть равна правой, то принадлежит, и наоборот.
1) у = х² - х +1 А(0; -1)
-1 = 0² - 0 + 1
-1 ≠ 1, не принадлежит.
2) у = х² - х +1 В(0; 1)
1 = 0² - 0 + 1
1 = 1, принадлежит.
3) у = х² - х +1 С(2; 0)
0 = 2² - 2 + 1
0 ≠ 3, не принадлежит.
4) у = х² - х +1 D(1; 1)
1 = 1² - 1 + 1
1 = 1, принадлежит.
5) у = х² - х +1 Е(-2; 6)
6 = (-2)² -(-2) + 1
6 ≠ 7, не принадлежит.
В обеих точках функция непрерывна
Объяснение:
Для ответа на данный вопрос найдём пределы слева и справа от указанных точек, если пределы совпадают, то функция в данной точке непрерывна, если не совпадают, то функция имеет разрыв первого рода, а если хотя бы один из пределов равен бесконечности или не существует, то в данной точке функция имеет разрыв второго рода.
для x = 0
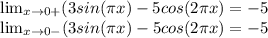
Как видим, пределы слева и справа совпадают, следовательно f(0) непрерывна
для x = 1
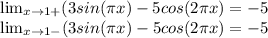
Снова видим, что пределы совпадают, следовательно и при f(1) функция непрерывна.
1. sin2x=sinx
2sinxcosx=sinx
2sinxcos-sinx=0
sinx(2cosx-1)=0
sinx=0 2cosx-1=0
x=Пn x=+-П\3+2Пn корня два следовательно решаем два неравенства
-3<Пn<3 |:П -3<п\3+2Пn<3 -3<-п\3+2Пn<3
-3\П<n<3\П переносим п\3 с противоположным знаком
следовательно -3-п\3<2Пn<3-П\3 |:2П -3+п\3<2Пn<3+п\3|:2П
~-0.95<n>~0.95 т.к П=3.14,то ~-0.63<n<~0.31 -3\2п+ 1\6<n<3\2п+1\6
n=0 следовательно n=0 -3\6.28+0.16<n<3\6.28+0.16
~-0.31<n<~0.63
следовательно n=0
Уравнение имеет три корня