Пусть скорость второго лыжника будет х км/ч, тогда скорость первого лыжника, будет х-2 км/ч (т.к. его скорость была на 2 км/ч меньше, чем у второго). Время, за которое первый лыжник преодолел расстояние в 40 км будет: 40/(х-2)=t Второй лыжник потратил столько же времени, сколько и первый, только преодолел 48 км, его время будет: 48/х=t
Т.к. время первого и второго лыжников равны, получаем уравнение: t=40/(х-2)=48/х
Решаем это уравнение относительно х: 40 = 48 х-2 х
40*х=48*(х-2) 40х=48х-48*2 40х=48х-96 48х-40х=96 8х=96 х=96:8 х=12 км/ч - скорость второго лыжника.
Скорость первого лыжника на 2 км/ч меньше, чем у второго, т.е.: 12-2=10 км/ч - скорость первого лыжника.
20 дней и 30 дней.
Объяснение:
Пусть один из сварщиков может выполнить всю работу за х дней,
тогда другой сварщик - за (25 * 2 - х) дней или (50 - х) дней.
Примем всю работу за 1, тогда производительность труда у первого сварщика равна 1/х, у второго сварщика -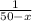 .
.
Совместна производительность труда двух сварщиков равна:
Составим уравнение и решим его:
1) x - 20 = 0
x = 20 (дней)
2) x - 30 = 0
x = 30 (дней)
Допустим, что один из сварщиков может выполнить всю работу за 20 дней, тогда второй сварщик может выполнить всю работу за:
50 - 20 = 30 (дней) и наоборот.