Докажите, что возрастающая или убывающая функция приобретает каждого своего значения только в одной точке ее области определения. Доведіть, що зростаюча або спадна функція набуває кожного свого значення тільки в одній точці її області визначення.
Пусть функция возрастает на всей области определения.
Предположим, что для некоторых значений аргумента и выполняется соотношение . Рассмотрим три ситуации:
1. - но по определению возрастающей функции меньшему значению аргумента соответствует меньшее значение функции: - противоречие вышеприведенному равенству значений функции
2. - две точки равны между собой, значит и значения функции в них также равны, вышеприведенное равенство выполняется
3. - аналогично, по определению возрастающей функции большему значению аргумента соответствует большее значение функции: - противоречие вышеприведенному равенству значений функции
Таким образом, при любых не может выполняться равенство . Это означает, что возрастающая функция не может принимать одно и то же значение в двух различных точках. Или по другому, возрастающая функция принимает каждое свое значение только в одной точке.
Для убывающей функции доказательство аналогичное с той лишь разницей, что случаю соответствует условие , а случаю - условие . Но опять же, разным значениям аргумента не могут соответствовать равные значения функции.
Давай обозначим скорость катера буквой v, и посмотрим время, которое катер шёл против течения t1 = 3 км / ( v - 2 )
а какое время катер шёл по течению? t2 = 20 км / ( v + 2 )
а какое время катер шёл по озеру? t = 21 км / v
Раз катер ходил туды-сюды по реке столько же времени, сколько и по озеру, то t1 + t2 = t подставляем 3 / ( v-2) + 20 / (v+2) = 21 / v
получаем уравнение, которое нужно просто решить. Ты можешь решить любым наверное лучше как учили в школе через дискриминант (ибо уравнение квадратное), а я лучше накидал табличку в экселе, и получил два решения: v = 3 и v = 14
При любом из этих двух значений скорости заданные условия выполнятся. Итого, ответ я написал бы так: скорость катера v = { 3 ; 14 } км/ч
Да, смотрится необычно, но что поделать. Решений-то два, и оба положительные :(
Пусть функция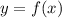 возрастает на всей области определения.
возрастает на всей области определения.
Предположим, что для некоторых значений аргумента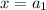 и
и 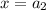 выполняется соотношение
выполняется соотношение 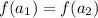 . Рассмотрим три ситуации:
. Рассмотрим три ситуации:
1.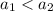 - но по определению возрастающей функции меньшему значению аргумента соответствует меньшее значение функции:
- но по определению возрастающей функции меньшему значению аргумента соответствует меньшее значение функции: 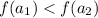 - противоречие вышеприведенному равенству значений функции
- противоречие вышеприведенному равенству значений функции
2. - две точки равны между собой, значит и значения функции в них также равны, вышеприведенное равенство выполняется
- две точки равны между собой, значит и значения функции в них также равны, вышеприведенное равенство выполняется
3.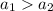 - аналогично, по определению возрастающей функции большему значению аргумента соответствует большее значение функции:
- аналогично, по определению возрастающей функции большему значению аргумента соответствует большее значение функции: 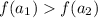 - противоречие вышеприведенному равенству значений функции
- противоречие вышеприведенному равенству значений функции
Таким образом, при любых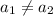 не может выполняться равенство
не может выполняться равенство 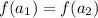 . Это означает, что возрастающая функция не может принимать одно и то же значение в двух различных точках. Или по другому, возрастающая функция принимает каждое свое значение только в одной точке.
. Это означает, что возрастающая функция не может принимать одно и то же значение в двух различных точках. Или по другому, возрастающая функция принимает каждое свое значение только в одной точке.
Для убывающей функции доказательство аналогичное с той лишь разницей, что случаю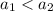 соответствует условие
соответствует условие 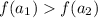 , а случаю
, а случаю 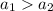 - условие
- условие 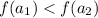 . Но опять же, разным значениям аргумента не могут соответствовать равные значения функции.
. Но опять же, разным значениям аргумента не могут соответствовать равные значения функции.