
Объём V тела (но не фигуры) равен объёму V1 тела, образованного вращением вокруг оси Ох криволинейной трапеции, ограниченной графиком функции у = х^3 минус объём V2 конуса, направляющая которого - это касательная к графику кривой.
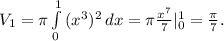
Объём конуса 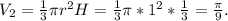
Решение: 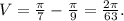
Высота конуса Н = 1/3 определена по разности х = 1 (граница фигуры на графике) и х =(2/3) как точка пересечения касательной оси Ох.
Уравнение касательной у(кас) = y'(x - xo) + yo.
y' = 3x², y'(1) = 3,
y(1) = 1³ = 1.
Уравнение касательной: у = 3(х - 1) + 1 = 3х - 3 + 1 = 3х -2.
Отсюда при у = 0 получаем х = (2/3).
45 = 9 * 5
1) Какие числа деляться на 5? Те, у которых на конце стоит 0 или 5
2) Какие числа деляться на 9? Те, у которых сумма вех цифр кратна 9
3) => Выпишем все возможные числа:
Но надо подумать 3 + 7 + 4 = 14... Чтобы число стало кратно 9 надо, чтобы сумма была равна 27(ближайшему кратному числу):
На конце должно стоять либо 0 или 5(рассмотрим 2-ва варианта):
1') Если стоит на конце 0 значит первая цифра 13. НО ЭТО НЕ ЦИФРА!
Следовательно это вариант не подходит!
2') Если стоит на конце 5 значит перфая цифра 8 и число получится 83745 И оно нам подходит!
ответ: 83745