y=1+x3, х∈(-∞;+∞) или D=(-∞;+∞)
y=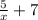
, х∈(-∞;0)∪(0;+∞) или D=(-∞;0)∪(0;+∞)
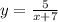, х∈(-∞;-7)∪(-7;+∞) или D=(-∞;-7)∪(-7;+∞)
Объяснение:
Область определения функции - откуда до куда твой график существует по оси Х.
а) y=1+x3 график прямой х∈(-∞;+∞)
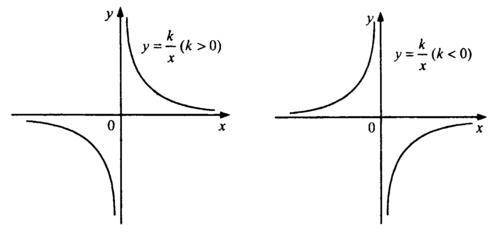
б) y=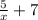 график гиберболы х∈(-∞;0)∪(0;+∞)
Если функция имеет вид: 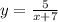то х∈(-∞;-7)∪(-7;+∞)
Знаменатель х+7 говорит о том, что асимптота сдвинута по оси х влево.
Можно записывать ответ по разному, два варианта записи ответа, необходимо выбрать 1:
y=1+x3, (1вариант) х∈(-∞;+∞) или (2 вариант) D=(-∞;+∞)
y=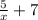, (1вариант) х∈(-∞;0)∪(0;+∞) или (2 вариант) D=(-∞;0)∪(0;+∞)
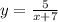, (1вариант) х∈(-∞;-7)∪(-7;+∞) или (2 вариант) D=(-∞;-7)∪(-7;+∞)
sqrt-корень квадратный , ^-степень
расписываешь cos6x и sin6x как cos ,sin половинного угла получается
cos12x=sqrt((1+cos12x)/2)+sqrt((1-cos12x)/2)
возводим обе части в квадрат получаем
cos(^2)(12x)=(1+cos12x+1-cos12x)/2+sqrt((1+cos12x)*(1-cos12x)/4) упрощаем
cos(^2)12x=1+ sqrt((1+cos12x)*(1-cos12x)/4)
переносим 1 влево и далее возводим обе части в квадрат получаем
(cos(^2)12x-1)^2=(1^2-cos(^2)12x)/4
возводим левую часть в квадрат и переносим 4
влево тогда получается
4*cos(^4)12x-8*cos(^2)12x+4=1-cos(^2)12x переносим все влево получается
4*cos(^4)12x-7*cos(^2)12x+3=0
пусть cos(^2)12x=t; t>=0 и t<=1
подставляем в биквадратное уравнение
4*t(^2)-7*t+3=0
находим дискриминант и корни
t1=(7+1)/8=8/8=1
t2=(7-1)/8=6/8=3/4
делаем обратную замену t на cos(^2)12x
1) cos(^2)12x=1
а)cos12x=-1 x=П/12+Пк/6
б)cos12x=1 x=Пк/6
2)cos(^2)12x=3/4
а)cos12x=sqrt(3)/2 x=П/72+Пк/6 x=-П/72+Пк/6
б)cos12x=-sqrt(3)/2 x=5*П/72+Пк/6 x=-5*П/72+Пк/6
x1=П/12+Пк/6,
x2=Пк/6
x3=П/72+Пк/6
x4=-П/72+Пк/6
x5=5*П/72+Пк/6
x6=-5*П/72+Пк/6
где к принадлежит N