ответ: ymin=y(-4)=-164
Объяснение:
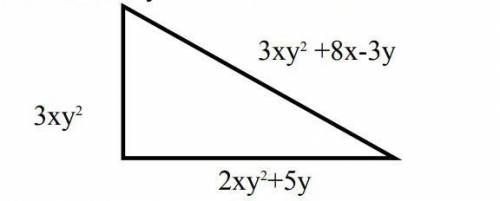
Найдите наименьшее значение функции у = х³ - 5х² + 8х + 12 на отрезке [-4;1].
Найдем значение функции на границах отрезка
у(-4) = (-4)³ - 5·(-4)² +8·(-4) + 12 = -64 - 80 - 32 + 12 = -164
у(1) = 1³ - 5·1² +8·1 + 12 = 1 - 5 + 8 + 12 = 16
Найдем производную функции
у' =(х³ - 5х² + 8х + 12)' = (х³)' - (5х²)' + (8х)' + (12)' = 3x² - 10x +8
Найдем критические точки приравняв производную к нулю
3x² - 10x + 8 = 0
D = (-10)² - 4·3·8 = 100 - 96 = 4
x₁ = (10-2)/(2·3) = 8/6 = 4/3 ≈ 1,33
x₂ = (10+2)/(2·3) = 12/6 = 2
Найденные точки не входят в данный отрезок поэтому значения функции в них находить не будем.
Функция на отрезке монотонна и возрастает. Минимальное значение функции находится в точке x = -4 y(-4) = -164
![РЕШИТЬ.Найдите наименьшее значение функции у=х^3-5х^2+8х+12 на отрезке [-4;1].](/tpl/images/1353/3405/90f6a.jpg)
Искомая функция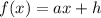 
.
Найдем значения искомой функции в заданных точках х:
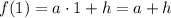
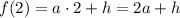
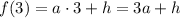
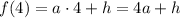
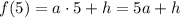
Кроме этого, для каждого из аргументов есть еще и экспериментальное значение, которое обозначим через функцию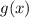 
:
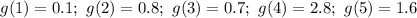
Составим функцию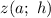 
, которая будет суммировать квадраты разностей значений функций 
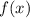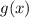и соответствующих аргументов:
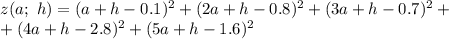
Исследуем эту функцию на экстремум.
Найдем частные производные:
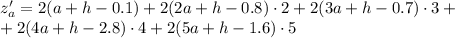
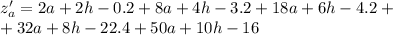
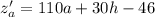
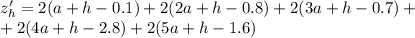
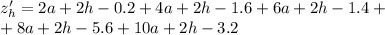
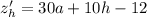
Необходимое условие экстремума: равенство нулю частных производных:
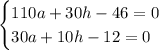
Домножим второе уравнение на (-3):
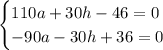
Складываем уравнения:
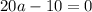
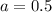
Подставим значение а во второе уравнение исходной системы:
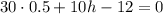
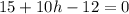
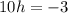
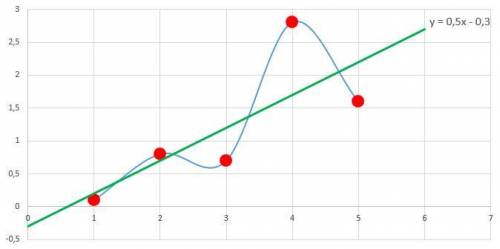
Точка (0.5; -0.3) - предполагаемая точка экстремума.
Найдем вторые частные производные функции:
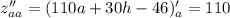
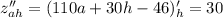
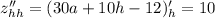
Рассмотрим выражение:
Так как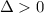 
и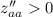 
, то точка (0.5; -0.3) является точкой минимума.
Значит, в точке (0.5; -0.3) функция 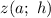имеет минимум.
Тогда, значения 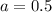и есть искомые коэффициенты функции .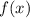
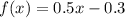
ответ: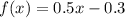
Привет)
Решение во вложении, будут вопросы, задавай)
Если не сложно, отметь как лучший ответ))
Объяснение: