
Подставляем значения точек в функцию
1) M(0;-корень3) значит
-корень3 = -ctg( 0+п/3)
-корень3 = -ctg п/3
-ctg п/3 сам по себе равен -1/-корень3
Следовательно -корень3 НЕ= -1/-корень3 , это неравенство, они не равны.
ЗНАЧИТ точка M(0;-корень3) не принадлежит графику данной функции
2) P(п/6;0) значит
0 = -ctg( п/6+п/3) , значения в скобках приводим к общему знаменателю получается 0 = -ctg п/2
-ctg п/2 каким бы он ни был ( положительным или отрицательным) он равен 0
Следовательно 0=0
ЗНАЧИТ точка P(п/6;0) принадлежит графику данной функции
x ≠ 0
Находи точки экстремума, для этого приравниваем производную к нулю.
-3 входит в данный промежуток, надо определить это точка макимума или минимума. Для этого берем любое значение из данного промежутка, например, -2, справа от этой точки, и подставляем его в производную и смотрим знак.
y'(-2) < 0
Значит х = -3 является точкой максимума. Т.е в этом промежутке и в этой точке находится наибольшее значение функции. Подставляем -3 в функцию.
y(-3) =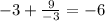
Находи точки экстремума, для этого приравниваем производную к нулю.
-2 входит в данный промежуток, надо определить это точка макимума или минимума. Для этого берем любое значение из данного промежутка, например, 0, справа от этой точки, и подставляем его в производную и смотрим знак.
y(0) < 0
Значит х = -2 является точкой максимума. Т.е в этом промежутке и в этой точке находится наибольшее значение функции. Подставляем -2 в функцию.
y(-2) =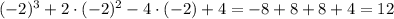
Про второй номер, к сожалению не смогу.