Пусть необходимое количество 20%-ного раствора будет х л, а 70%-ного - у л. Тогда всего надо взять х+у или 100 л. Содержание соляной кислоты в 20%-ном растворе будет 0,2х, в 70%-ном - 0,7у, а в полученном 50%-ном - 0,5*100 л или 0,2х+0,7у. Составим и решим систему уравнений:
х+у=100
0,2х+0,7у=0,5*100 |*10
х=100-у
2x+7у=500
х=100-у
2(100-у)+7у=500
х=100-у
200-2у+7у=500
х=100-у
5у=500-200
х=100-у
5у=300
х=100-у
у=300:5
х=100-у
у=60
х=100-60
у=60
х=40
у=60
ответ: для того, чтобы получить 100 л 50%-ного раствора соляной кислоты, необходимо взять 40 литров её 20%-ного раствора и 60 литров 70%-ного раствора.
1) область определения
Функция определена и непрерывна на всей числовой прямой
D(y)=R
(Это очень хорошо, отпадают вертикальные асимптоты)
2) Проверим функцию на чётность/нечётность
значит, данная функция не является чётной или нечётной.
Очевидно, что функция непериодическая.(т.к. она не является тригонометрической)
3) Асимптоты, поведение функции на бесконечности.
Так как функция непрерывна на R , то вертикальные асимптоты отсутствуют.
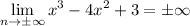
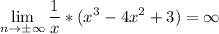
Так как пределы бесконечны, горизонтальных асимптот нет
Найдем вертикальные асимптоты
Значит наклонных асимптот тоже нет
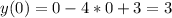
4) Определим точки пересечения графика функции с осями координат
х=0
Пересечение с осью ОУ в точке (0;3)
у=0
Пересечение с осью ОХ (1;0) ; (√3;0) ; (-√3;0)
5) Исследуем функцию на экстремумы и монотонность. Для этого найдем первую производную функции
Точки х=0 и х=8/3 точки экстремума функции
__+_____0______-____8/3___+__
возр убыв возр
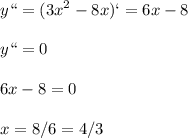
Значит х= 0 точка максимума у(0)=3
Значит точка х=8/3 точка минимума у(8/3)= -175/27
на промежутке (-оо; 0) возрастает
на промежутке (0; 8/3) убывает
на промежутке (8/3; +oo) возрастает
6) Исследуем функцию на перегибы и выпуклость
значит х=4/3 точка перегиба
_-_____ 4/3__+____
выпуклая/ вогнутая
7) Дополнительные точки. Вычислим значение функции в некоторых других точках, чтобы точнее построить график.
х=2 y(1)=2³-4*2²+3=8-16+3= -5
х= -2 y(-2)= (-2)³-4*(-2)²+3=-8-16+3=-21
теперь по полученным данным построим график