Выражение: (a-b-c)^2=a^2+b^2+c^2+2*b*c-2*a*b-2*a*c
ответ: 0=0
Решаем по действиям:
1. (a-b-c)^2=a^2-2*a*b-2*a*c+b^2+2*b*c+c^2
(a-b-c)^2=((a-b-c)*(a-b-c))
1.1. (a-b-c)*(a-b-c)=a^2-2*a*b-2*a*c+b^2+2*b*c+c^2
(a-b-c)*(a-b-c)=a*a-a*b-a*c-b*a+b*b+b*c-c*a+c*b+c*c
1.1.1. a*a=a^2
a*a=a^(1+1)
1.1.1.1. 1+1=2
+1
_1_
2
1.1.2. -a*b-b*a=-2*a*b
1.1.3. b*b=b^2
b*b=b^(1+1)
1.1.3.1. 1+1=2
+1
_1_
2
1.1.4. -a*c-c*a=-2*a*c
1.1.5. b*c+c*b=2*b*c
1.1.6. c*c=c^2
c*c=c^(1+1)
1.1.6.1. 1+1=2
+1
_1_
2
2. a^2-a^2=0
3. b^2-b^2=0
4. c^2-c^2=0
5. 2*b*c-2*b*c=0
6. -2*a*b+2*a*b=0
7. -2*a*c+2*a*c=0
Решаем по шагам:
1. a^2-2*a*b-2*a*c+b^2+2*b*c+c^2-a^2-b^2-c^2-2*b*c+2*a*b+2*a*c=0
1.1. (a-b-c)^2=a^2-2*a*b-2*a*c+b^2+2*b*c+c^2
(a-b-c)^2=((a-b-c)*(a-b-c))
1.1.1. (a-b-c)*(a-b-c)=a^2-2*a*b-2*a*c+b^2+2*b*c+c^2
(a-b-c)*(a-b-c)=a*a-a*b-a*c-b*a+b*b+b*c-c*a+c*b+c*c
1.1.1.1. a*a=a^2
a*a=a^(1+1)
1.1.1.1.1. 1+1=2
+1
_1_
2
1.1.1.2. -a*b-b*a=-2*a*b
1.1.1.3. b*b=b^2
b*b=b^(1+1)
1.1.1.3.1. 1+1=2
+1
_1_
2
1.1.1.4. -a*c-c*a=-2*a*c
1.1.1.5. b*c+c*b=2*b*c
1.1.1.6. c*c=c^2
c*c=c^(1+1)
1.1.1.6.1. 1+1=2
+1
_1_
2
2. -2*a*b-2*a*c+b^2+2*b*c+c^2-b^2-c^2-2*b*c+2*a*b+2*a*c=0
2.1. a^2-a^2=0
3. -2*a*b-2*a*c+2*b*c+c^2-c^2-2*b*c+2*a*b+2*a*c=0
3.1. b^2-b^2=0
4. -2*a*b-2*a*c+2*b*c-2*b*c+2*a*b+2*a*c=0
4.1. c^2-c^2=0
5. -2*a*b-2*a*c+2*a*b+2*a*c=0
5.1. 2*b*c-2*b*c=0
6. -2*a*c+2*a*c=0
6.1. -2*a*b+2*a*b=0
7. 0=0
7.1. -2*a*c+2*a*c=0
Объяснение:
1я бригада 300 дет/час
2я бригада 300 -х дет/час
3я бригада 300 +4х дет/час
время выполнения работы
t=((1/4)/(300+300-x)) + ((3/4)/(300+300-x+300+4x))=
=(1/4)[900+3x+3(600-x)]/((600-x)(900+3x))=
=(2700/4)[1/(-3x²+900x+540000)]
t будет иметь минимальное значение при максимальном значении выражения -3x²+900x+540000
по свойству квадратичной функции так как коэффициент при х² меньше 0 то ветки параболы направлены вниз и максимум квадратичной функции будет в вершине
х=-b/2a=900/6=150 деталей в час
Объяснение:
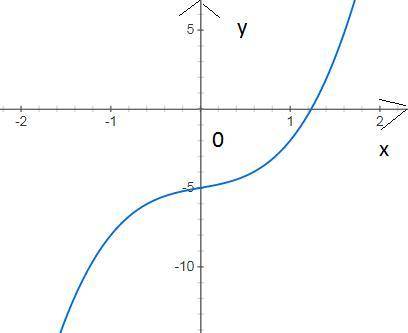
y=2x^3+x-5
1) D(y)=R
2) функция общего вида
y(-x)=-2x³-x-5 ≠y(x) и ≠-у(х)
функция общего вида
3)
∩ с ОУ
х=0 у=-5 (0;-5)
∩ с ОX
2x^3+x-5=0 кубическое уравнение решать долго не буду тратить на это время. Но если так уж надо то можно и решить, но для исследования функции вопрос непринципиальный. (Если все-таки надо то см. приложение Нули функции.)
Подставляя различные значения х можно определить численно
что при х≤1 у<0 а при х≥2 у >0
у(1)=-2 у(2)= 13
значит вещественный корень х₀ находится между 1 и 2
два других корня по видимому комплексные
значит точка пересечения с ОХ между 1 и 2
4) Промежутки знакопостоянства
(-∞ ; х₀) у<0
(х₀; +∞) y>0
5) монотонность
у'=6x²+1>0
функция возрастает на всей области определения
Дополнительно
6)
в образце решения отсутствует выпуклость вогнутость
но на всякий случай исследуем этот вопрос если не надо можете пропустить
y''=12x=0 ; x=0
при х<0 y''<0 график выпуклый вверх
при х>0 y'>0 график вогнутый вниз
у(0)=-5
(0;-5) точка перегиба

Выражение: (a-b-c)^2=a^2+b^2+c^2+2*b*c-2*a*b-2*a*c
ответ: 0=0
Решаем по действиям:
1. (a-b-c)^2=a^2-2*a*b-2*a*c+b^2+2*b*c+c^2
(a-b-c)^2=((a-b-c)*(a-b-c))
1.1. (a-b-c)*(a-b-c)=a^2-2*a*b-2*a*c+b^2+2*b*c+c^2
(a-b-c)*(a-b-c)=a*a-a*b-a*c-b*a+b*b+b*c-c*a+c*b+c*c
1.1.1. a*a=a^2
a*a=a^(1+1)
1.1.1.1. 1+1=2
+1
_1_
2
1.1.2. -a*b-b*a=-2*a*b
1.1.3. b*b=b^2
b*b=b^(1+1)
1.1.3.1. 1+1=2
+1
_1_
2
1.1.4. -a*c-c*a=-2*a*c
1.1.5. b*c+c*b=2*b*c
1.1.6. c*c=c^2
c*c=c^(1+1)
1.1.6.1. 1+1=2
+1
_1_
2
2. a^2-a^2=0
3. b^2-b^2=0
4. c^2-c^2=0
5. 2*b*c-2*b*c=0
6. -2*a*b+2*a*b=0
7. -2*a*c+2*a*c=0
Решаем по шагам:
1. a^2-2*a*b-2*a*c+b^2+2*b*c+c^2-a^2-b^2-c^2-2*b*c+2*a*b+2*a*c=0
1.1. (a-b-c)^2=a^2-2*a*b-2*a*c+b^2+2*b*c+c^2
(a-b-c)^2=((a-b-c)*(a-b-c))
1.1.1. (a-b-c)*(a-b-c)=a^2-2*a*b-2*a*c+b^2+2*b*c+c^2
(a-b-c)*(a-b-c)=a*a-a*b-a*c-b*a+b*b+b*c-c*a+c*b+c*c
1.1.1.1. a*a=a^2
a*a=a^(1+1)
1.1.1.1.1. 1+1=2
+1
_1_
2
1.1.1.2. -a*b-b*a=-2*a*b
1.1.1.3. b*b=b^2
b*b=b^(1+1)
1.1.1.3.1. 1+1=2
+1
_1_
2
1.1.1.4. -a*c-c*a=-2*a*c
1.1.1.5. b*c+c*b=2*b*c
1.1.1.6. c*c=c^2
c*c=c^(1+1)
1.1.1.6.1. 1+1=2
+1
_1_
2
2. -2*a*b-2*a*c+b^2+2*b*c+c^2-b^2-c^2-2*b*c+2*a*b+2*a*c=0
2.1. a^2-a^2=0
3. -2*a*b-2*a*c+2*b*c+c^2-c^2-2*b*c+2*a*b+2*a*c=0
3.1. b^2-b^2=0
4. -2*a*b-2*a*c+2*b*c-2*b*c+2*a*b+2*a*c=0
4.1. c^2-c^2=0
5. -2*a*b-2*a*c+2*a*b+2*a*c=0
5.1. 2*b*c-2*b*c=0
6. -2*a*c+2*a*c=0
6.1. -2*a*b+2*a*b=0
7. 0=0
7.1. -2*a*c+2*a*c=0
Решаем уравнение 0=0: примечания. в начале решения там подпунктики где 1.1.1 их можно и не писать, если решение нужно не полное