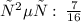

Отрезок AC называется перпендикуляром, проведённым из точки A прямой a , если прямые AC и a перпендикулярны.
пер3.jpg
Точка C называется основанием перпендикуляра.
От точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Perpendikuls.png Perpendikuls1.png
Докажем, что от точки A , не лежащей на прямой BC , можно провести перпендикуляр к этой прямой.
Допустим, что дан угол ∡ABC .
Отложим от луча BC угол, равный данному, и совместим эти углы накладыванием (представим, что сложим лист бумаги с равными углами по стороне BC ).
Сторона BA совместится со стороной BA1 .
При этом точка A наложится на некоторую точку A1 .
Следовательно, совмещается угол ∡ACB с ∡A1CB .
Но углы ∡ACB и ∡A1CB — смежные, значит, каждый из них прямой.
Прямая AA1 перпендикулярна прямой BC , а отрезок AC является перпендикуляром от точки A к прямой BC .
Если допустить, что через точку A можно провести ещё один перпендикуляр к прямой BC , то он бы находился на прямой, пересекающейся с AA1 . Но две к одной и той же прямой перпендикулярные прямые должны быть параллельны и не могут пересекаться.
Это противоречие, что означает: через данную точку к прямой можно провести только один перпендикуляр.
Медианы, биссектрисы и высоты треугольника
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Поэтому для построения медианы необходимо выполнить следующие действия:
1. найти середину стороны;
2. соединить точку, являющуюся серединой стороны треугольника, с противолежащей вершиной отрезком — это и будет медиана.
Mediana.png
У треугольника три стороны, следовательно, можно построить три медианы.
Все медианы пересекаются в одной точке.
Mediana1.png
Биссектриса треугольника — это отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне.
Поэтому для построения биссектрисы необходимо выполнить следующие действия:
1. построить биссектрису какого-либо угла треугольника (биссектриса угла — это луч, выходящий из вершины угла и делящий его на две равные части);
2. найти точку пересечения биссектрисы угла треугольника с противоположной стороной;
3. соединить вершину треугольника с точкой пересечения на противоположной стороне отрезком — это и будет биссектриса треугольника.
Bisektrise.png
У треугольника три угла и три биссектрисы.
Все биссектрисы пересекаются в одной точке.
Bisektrise1.png
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противоположную сторону.
Поэтому для построения высоты необходимо выполнить следующие действия:
1. провести прямую, содержащую одну из сторон треугольника (в случае, если проводится высота из вершины острого угла в тупоугольном треугольнике);
2. из вершины, лежащей напротив проведённой прямой, опустить перпендикуляр к ней (перпендикуляр — это отрезок, проведённый из точки к прямой, составляющей с ней угол 90° ) — это и будет высота.
Augstums.png
Так же как медианы и биссектрисы, треугольник имеет три высоты.
Высоты треугольника пересекаются в одной точке.
Augstums1.png
Но, как выше упомянуто, для некоторых видов треугольников построение высот и точки их пересечения отличаются.
Если треугольник с прямым углом, то стороны, образующие прямой угол, можно назвать высотами, так как они перпендикулярны одна к другой. Точкой пересечения высот является общая вершина перпендикулярных сторон.
Augstums2.png
Объяснение:
Объяснение: