Теңдеулер жүйесін алмастыру тәсілімен шешініздер: x-2у-4=0 х²-2у²=16 - id1443162920210111 от mariarura 11.01.2021 17:20

Question

Алгебра: Теңдеулер жүйесін алмастыру тәсілімен шешініздер: x-2у-4=0 х²-2у²=16​

mariarura · Accepted Answer

(-бесконечности ; -10] и (7; +бесконечности)

Объяснение:

Запишем все под одной дробью:

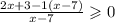
$\frac{2x + 3 - 1(x - 7)}{x - 7} \geqslant 0$

Найдём область допустимых значений:

х-7≠0, то есть х ≠ 7

Раскроем скобки и решим:

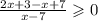
$\frac{2x+ 3 - x + 7}{x - 7} \geqslant 0$

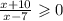
$\frac{x + 10}{x - 7} \geqslant 0$

Рассмотрим все возможные случаи (знаменатель строго больше нуля, так как если он будет равен нулю, выражение потеряет смысл):

1. Когда и знаменатель, и числитель больше 0

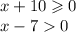
$x + 10 \geqslant 0 \\ x - 7 0$

2. Когда оба меньше 0

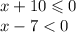
$x + 10 \leqslant 0 \\ x - 7 < 0$

1.

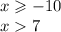
$x \geqslant - 10 \\ x 7$

То есть х принадлежит ( 7; +бесконечности)

Так как 7 не удовлетворяет ОДЗ, то скобки круглые

2.

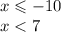
$x \leqslant - 10 \\ x < 7$

То есть х принадлежит (- бесконечности ; - 10]

Найдём объединение:

Х принадлежит (-бесконечности ; -10] и (7; +бесконечности)

Теңдеулер жүйесін алмастыру тәсілімен шешініздер: x-2у-4=0х²-2у²=16​