Алгебра: разложите на множетели а^2в-3ав+6а-18+ав-3в

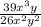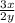
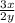
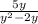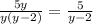
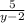
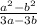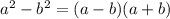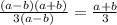
Задание №1а). (сокращаем на 13y )ответ: б). (в знаменателе выносим y и сокращаем с y в числителе)ответ: в). (раскрываем числитель по формуле разности квадратов , в знаменателе выносим 3 )ответ: 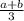Задание №2а). 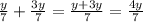(одинаковый знаменатель, значит можно складывать)ответ: 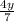б). 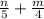(знаменатели разные, чтобы сложить приводим к общему знаменателю. 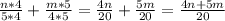Первую дробь умножаем на 4, вторую умножаем на 5, после чего складываем)ответ: 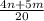в). (принцип тот же. а есть и там, и там в знаменателе, значит первую дробь умножаем на...

разложите на множетели а^2в-3ав+6а-18+ав-3в

👇

Увидеть ответ

Открыть все ответы

Ответ:

Luuunar

01.12.2020

1. y=-2/x+1 (График №1)
ОДЗ: x+1≠0 => x≠-1
D(f)=x∈(-∞;-1)∪(-1;+∞)
2. y=2x²-2х-3 (График №2)
а) промежуток возрастания:(-∞;0.5)
промежуток убывания:(0.5;+∞)
(f`(x)=4x-2; x=0.5 - экстремум)
б) наименьшее значение функции: y=-3
в) y<0 при -1<х<2
3. -х²-2х+8=0
f(x)=-x^2-2x+8 (График №3)
x₁=-4
x₂=2
4. {y=-√х+3 (График №4)
{y=|x-3|
ОДЗ: x≥0
x₁=0; y₁=3
x₂=1; y₂=2
x₃=4; y₃=1
5.y=х²+px-24
Точка (4;0) принадлежит данной параболе
0=4²+р*4-24
16+4p-24=0
4p=8
p=2
f(x)=x²+2x-24 (График №5)
ось симметрии проходит через вершину параболы,
координаты вершины параболы:
x₀=-b/2a
-2/2*1=-1
y₀=-D/4a
D=2²-4*1*(-24)=100
-100/4*1=-25
Координаты вершины (-1;-25)
Уравнение оси симметриии параболы: х=-1
1.постройте график функции y=-2/x+1. укажи область определения функции 2.постройте график функции y=

1.постройте график функции y=-2/x+1. укажи область определения функции 2.постройте график функции y=

4,5(33 оценок)

Ответ:

Selebruty1

01.12.2020

Задание №1

а). $\frac{39x^{3}y }{26x^{2} y^{2} }$ (сокращаем на "13 $x^{2}$ y")

$\frac{3x}{2y}$

ответ: $\frac{3x}{2y}$

б). $\frac{5y}{y^{2}-2y }$ (в знаменателе выносим "y" и сокращаем с "y" в числителе)

$\frac{5y}{y(y-2)} = \frac{5}{y-2}$

ответ: $\frac{5}{y-2}$

в). $\frac{a^{2}-b^{2} }{3a-3b}$ (раскрываем числитель по формуле разности квадратов $a^{2} -b^{2} = (a-b)(a+b)$ , в знаменателе выносим "3")

$\frac{(a-b)(a+b)}{3(a-b)} = \frac{a+b}{3}$

ответ: $\frac{a+b}{3}$

Задание №2

а). $\frac{y}{7}+\frac{3y}{7} = \frac{y+3y}{7} = \frac{4y}{7}$ (одинаковый знаменатель, значит можно складывать)

ответ: $\frac{4y}{7}$

б). $\frac{n}{5}+\frac{m}{4}$ (знаменатели разные, чтобы сложить приводим к общему знаменателю. Первую дробь умножаем на 4, вторую умножаем на 5, после чего складываем)

$\frac{n*4}{5*4}+\frac{m*5}{4*5}= \frac{4n}{20} +\frac{5m}{20} = \frac{4n+5m}{20}$

ответ: $\frac{4n+5m}{20}$

в). $\frac{3}{2a}-\frac{5}{3a}$ (принцип тот же. "а" есть и там, и там в знаменателе, значит первую дробь умножаем на 3, вторую умножаем на 2, чтобы получить общий знаменатель, после чего вычитаем)

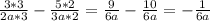
$\frac{3*3}{2a*3}-\frac{5*2}{3a*2} = \frac{9}{6a}-\frac{10}{6a} = -\frac{1}{6a}$

ответ: 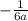$-\frac{1}{6a}$

г). 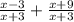$\frac{x-3}{x+3}+\frac{x+9}{x+3}$ (знаменатель одинаковый - складываем)

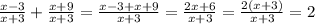
$\frac{x-3}{x+3}+\frac{x+9}{x+3} = \frac{x-3+x+9}{x+3}= \frac{2x+6}{x+3}=\frac{2(x+3)}{x+3} = 2$

ответ: 2

Задание №3

а). 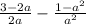$\frac{3-2a}{2a} -\frac{1-a^{2} }{a^{2} }$ (умножаем первую дробь на a, а вторую умножаем на 2, после чего вычитаем дроби)

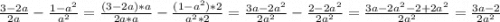
$\frac{3-2a}{2a} -\frac{1-a^{2} }{a^{2} } = \frac{(3-2a)*a}{2a*a}-\frac{(1-a^{2})*2}{a^{2}*2} = \frac{3a-2a^{2} }{2a^{2} } -\frac{2-2a^{2} }{2a^{2} } = \frac{3a-2a^{2}-2+2a^{2} }{2a^{2} } = \frac{3a-2}{2a^{2} }$

ответ: 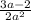$\frac{3a-2}{2a^{2} }$

б). $\frac{1}{3x+y}-\frac{1}{3x-y}$ (первую дробь умножаем на знаменатель второй дроби, а вторую дробь умножаем на знаменатель первой дроби, после чего вычитаем)

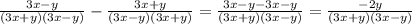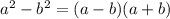$\frac{3x-y}{(3x+y)(3x-y)} -\frac{3x+y}{(3x-y)(3x+y)} = \frac{3x-y-3x-y}{(3x+y)(3x-y)}= \frac{-2y}{(3x+y)(3x-y)}$ (ещё можно свернуть по формуле разности квадратов $a^{2} -b^{2} = (a-b)(a+b)$ )

ответ: 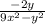$\frac{-2y}{9x^{2}-y^{2} }$

в). $\frac{3}{b-2}-\frac{4-3b}{b^{2}-2b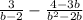}$ (вынесем "b" в знаменателе второй дроби за скобку и умножим первую дробь на "b", после чего вычитаем)

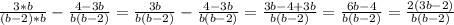
$\frac{3*b}{(b-2)*b}-\frac{4-3b}{b(b-2)} = \frac{3b}{b(b-2)} -\frac{4-3b}{b(b-2)} = \frac{3b-4+3b}{b(b-2)} = \frac{6b-4}{b(b-2)} = \frac{2(3b-2)}{b(b-2)}$

ответ: 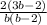$\frac{2(3b-2)}{b(b-2)}$

Задание №4

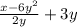$\frac{x-6y^{2} }{2y} +3y$ (приведем к общему знаменателю умножив 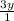$\frac{3y}{1}$ на "2y", после чего сложим)

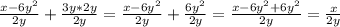$\frac{x-6y^{2} }{2y} +\frac{3y*2y}{2y} = \frac{x-6y^{2} }{2y} + \frac{6y^{2} }{2y} = \frac{x-6y^{2}+6y^{2} }{2y} = \frac{x}{2y}$ (теперь подставляем x = -8 и y = 0,1. Десятичное число 0,2 = дроби 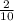$\frac{2}{10}$ . Когда получилась трёхэтажная дробь, то знаменатель дроби в знаменателе переносится в числитель и умножается на числитель общей дроби, а знаменатель становится числитель дроби в знаменателе)

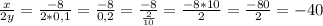
$\frac{x}{2y} = \frac{-8}{2*0,1}= \frac{-8}{0,2}= \frac{-8}{\frac{2}{10} } = \frac{-8*10}{2} = \frac{-80}{2} = -40$

ответ: -40

Задание №5

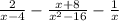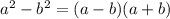$\frac{2}{x-4}-\frac{x+8}{x^{2}-16} -\frac{1}{x}$ (знаменатель средней дроби раскроем по формуле разности квадратов $a^{2} -b^{2} = (a-b)(a+b)$ .

Первую дробь умножим на "х" и на "x+4", среднюю дробь умножим на "х", а третью дробь умножим на "x+4" и на "x-4", после чего посчитаем)

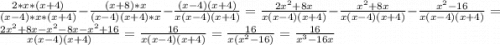$\frac{2*x*(x+4)}{(x-4)*x*(x+4)}-\frac{(x+8)*x}{(x-4)(x+4)*x} -\frac{(x-4)(x+4)}{x(x-4)(x+4)} = \frac{2x^{2}+8x}{x(x-4)(x+4)}-\frac{x^{2}+8x}{x(x-4)(x+4)}-\frac{x^{2}-16}{x(x-4)(x+4)} =\frac{2x^{2}+8x-x^{2}-8x-x^{2}+16}{x(x-4)(x+4)} =\frac{16}{x(x-4)(x+4)} = \frac{16}{x(x^{2}-16)} = \frac{16}{x^{3}-16x}$ ответ: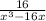 $\frac{16}{x^{3}-16x}$