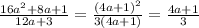Решить 1)корень 100/2 корень 40 2) х в квадрате -6х+9/х в квадрате-3х(сократить) 3)корень 18+корень 64- 4 корень 2 4) 8а-40/4а в квадрате-100 5) 5а+30/ а в квадрате-36 6) 4х+20/ х в квадрате+10х+25 7) корень 49х-3корень4х+корень х 8)16а в квадрате +8а+1/12а+3
1)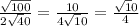
2)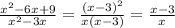
3)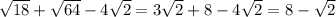
4)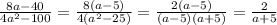
5)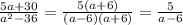
6)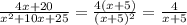
7)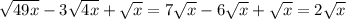
8)