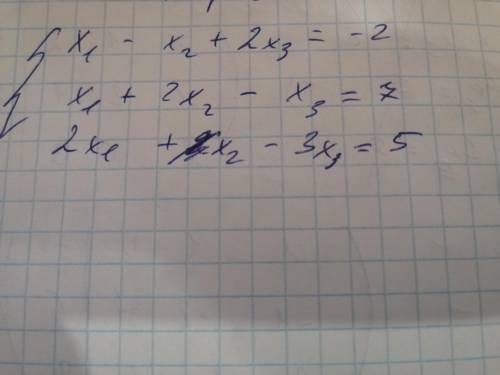
Смотри, ученика всего 23. У нас спрашивают, что сколько учеников имеет ТОЧНО более трёх конфет.
Нам сказано, что 7 из них имеют по 3 или менее конфет, а восемнадцать, по 2 или больше. А всего учеников-то 23!
2 или больше, может быть те восемнадцать имеют 3 конфеты, значит они входят в те 7. (ведь 7 учеников получили 3 или меньше, а 18 2 или больше, они могли получить 3 конфеты, ведь 2>3)
23-7=16 (конфет, которые ещё входят в список возможных детей, у которых больше 3-ёх конфет)
Но, ведь 18+7=25! А не 23, значит те, кто входят в число 18-ть (эти 2 человека из тех семи, кто имеет меньше двух конфет) Значит 2 человека ещё выпадают, у них по 3 или менее конфет. (Ведь нам не сказано, что 18 имеют по 3 или более, нам сказано, что 18 имеют 2 и более, значит могут иметь и 3 конфетки, и входить в число тех, кто получил меньше трёх, а не больше)
Значит 16-2=14 (ещё минус 2 человека)
Это число тех, кто точно имеет больше трёх конфет.
ответ: 14
Для такого задания есть два решения:
самый простой): проверить каждый вариант ответа, подставляя его вместо икса. Если получиться ноль, тогда это и есть корень уравнения.
При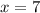
: 
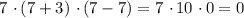(совпало)При 
: 
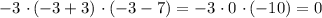(совпало)При 
: 
(совпало).решить это уравнение, зная правило, что если при умножении чисел или выражений получается ноль, то хотя бы одно из них должно быть равно нулю:
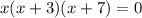
(в вариантах ответа есть такой корень)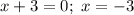
(в вариантах ответа есть такой корень)
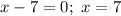(в вариантах ответа есть такой корень)ответ: корнем уравнения являются числа а) 7; б) -3; в) 0.
Объяснение:
x1 - x2 + 2x3 = -2
x1 + 2x2 - x3 = 7
2x1 + x2 - 3x3 = 5
Перепишем систему уравнений в матричном виде и решим его методом Гаусса
1 -1 2 -2
1 2 -1 7
2 1 -3 5
от 2 строки отнимаем 1 строку, умноженную на 1; от 3 строки отнимаем 1 строку, умноженную на 2
1 -1 2 -2
0 3 -3 9
0 3 -7 9
2-ую строку делим на 3
1 -1 2 -2
0 1 -1 3
0 3 -7 9
к 1 строке добавляем 2 строку, умноженную на 1; от 3 строки отнимаем 2 строку, умноженную на 3
1 0 1 1
0 1 -1 3
0 0 -4 0
3-ую строку делим на -4
1 0 1 1
0 1 -1 3
0 0 1 0
от 1 строки отнимаем 3 строку, умноженную на 1; к 2 строке добавляем 3 строку, умноженную на 1
1 0 0 1
0 1 0 3
0 0 1 0
x1 = 1
x2 = 3
x3 = 0
Сделаем проверку. Подставим полученное решение в уравнения из системы и выполним вычисления:
1 - 3 + 2·0 = 1 - 3 + 0 = -2
1 + 2·3 - 0 = 1 + 6 + 0 = 7
2·1 + 3 - 3·0 = 2 + 3 + 0 = 5
Проверка выполнена успешно.
x1 = 1
x2 = 3
x3 = 0
ЕСЛИ НЕ ПОНЯТНО, ТО ВОТ ССЫЛКА:https://ru.onlinemschool.com/math/assistance/equation/gaus/