Дано: F(x) = x² -2*x + 5, y(x)= x+3
Найти: S=? - площадь фигуры
Пошаговое объяснение:
1) Находим точки пересечения графиков: F(x)=y(x).
-x²+3*x-2=0 - квадратное уравнение
b = 2 - верхний предел, a = 1 - нижний предел.
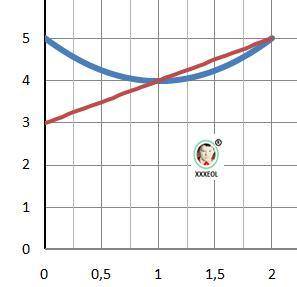
2) Площадь - интеграл разности функций. Прямая выше параболы.
s(x) = y(x) - F(x) = 2 -3*x + x² - подинтегральная функция
3) Интегрируем функцию и получаем:
S(x) = 2*x -3/2*x² + 1/3*x³
4) Вычисляем на границах интегрирования.
S(b) = S(2) = 4 -6 + 2,67 = 0,67
S(a) = S(1) = 2 -1,5 + 0,33 = 0,83
S = S(1)- S(2) = 0,16(ед.²) - площадь - ответ
Рисунок к задаче в приложении.
Очень маленькая площадь.
Разложим одночлены в сумму нескольких
x³-3x²+2x²-6x-2x+6=0
(x³-3x²)+(2x²-6x)-(2x-6)=0 - в скобки это сгруппировано для того чтоб вынести общий множитель
x²(x-3)+2x(x-3)-2(x-3)=0
(x-3)(x²+2x-2)=0
x-3=0
x1=3
x²+2x-2=0
Вычислим дискриминант
D=b²-4ac=2²-4*(-2)=12; √D = 2√3
x2=(-b+√D)/2a=(-2+2√3)/2=-1+√3
x3=(-b-√D)/2a=(-2-2√3)/2=-1-√3
ответ: -1-√3; -1+√3; 3.
4x⁴-8x³+3x²+2x-1=0
(4x⁴-8x³+3x²)+(2x-1)=0
(2x³-3x²+1)(2x-1)+(2x-1)=0
(2x³-3x²+1)(2x-1)=0
Произведение равно нулю
x³-3x²+1=0
Разложим опять же в сумму нескольких
2x³-2x²-x²+x-x+1=0
2x²(x-1)-x(x-1)-(x-1)=0
(x-1)(2x²-x-1)=0
x-1=0
x1=1
2x²-x-1=0|:2
x²-0.5x-0.5=0
По т. Виета
x2=-0.5
x3=1
2x-1=0
x4=0.5
ответ: -0.5; 0.5; 1.